题目内容
【题目】如图,四边形ABCD中,对角线AC⊥BD于点O,且AO=BO=4,CO=8,∠ADB=2∠ACB,则四边形ABCD的面积为( )
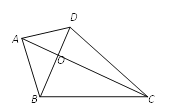
A.48B.42C.36D.32
【答案】B
【解析】
如图,作∠ADO的平分线DP交AC于P,作PE⊥AD于E.由△POD∽△BOC,得![]() ,设OP=x,推出OD=2x,由PE⊥AD,PO⊥DO,∠PDE=∠PDO,推出PE=OP,由
,设OP=x,推出OD=2x,由PE⊥AD,PO⊥DO,∠PDE=∠PDO,推出PE=OP,由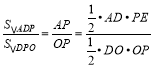 ,推出
,推出![]() ,推出AD=2(4-x),在Rt△ADO中,根据AD2=AO2+DO2,可得4(4-x)2=4x2+42,求出x的值,再根据S四边形ABCD=S△ABD+S△BDC=
,推出AD=2(4-x),在Rt△ADO中,根据AD2=AO2+DO2,可得4(4-x)2=4x2+42,求出x的值,再根据S四边形ABCD=S△ABD+S△BDC=![]() BDAO+
BDAO+![]() BDOC=
BDOC=![]() BD(OA+OC)计算即可.
BD(OA+OC)计算即可.
如图,作∠ADO的平分线DP交AC于P,作PE⊥AD于E.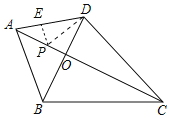
∵∠ADO=2∠BCO,
∴∠PDO=∠BCO,
∵∠POD=∠BOC,
∴△POD∽△BOC,
∴![]() ,设OP=x,
,设OP=x,
∴![]() ,
,
∴OD=2x,
∵PE⊥AD,PO⊥DO,∠PDE=∠PDO,
∴PE=OP,
∴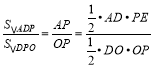 ,
,
∴![]() ,
,
∴AD=2(4-x),
在Rt△ADO中,∵AD2=AO2+DO2,
∴4(4-x)2=4x2+42,
∴x=![]() ,
,
∴OD=3,
∴S四边形ABCD=S△ABD+S△BDC=![]() BDAO+
BDAO+![]() BDOC=
BDOC=![]() BD(OA+OC)=
BD(OA+OC)=![]() ×7×12=42.
×7×12=42.
故选B.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
【题目】观察下表中的每一组值:
名称组别 |
|
|
| 名称组别 |
|
|
|
第1组 | 3 |
|
| 第5组 | |||
第2组 | 5 |
|
|
|
|
| |
第3组 | 7 |
|
|
|
|
| |
第4组 | 8 |
|
| 第 |
(1)根据表中前四组![]() 、
、![]() 、
、![]() 值的变化规律,第5组中
值的变化规律,第5组中![]() ;
;![]() ;第
;第![]() 组中
组中![]() ;
;![]() ;
;![]() .
.
(2)试证明以表中每组![]() 、
、![]() 、
、![]() 为边的三角形都是直角三角形.
为边的三角形都是直角三角形.