题目内容
【题目】对一个矩形ABCD及![]() 给出如下定义:在同一平面内,如果
给出如下定义:在同一平面内,如果![]() 上存在一点,使得这点到矩形ABCD的四个顶点的距离相等,那么称矩形ABCD是
上存在一点,使得这点到矩形ABCD的四个顶点的距离相等,那么称矩形ABCD是![]() 的“随从矩形”
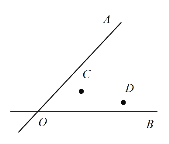
的“随从矩形”![]() 如图,在平面直角坐标系xOy中,直线l:
如图,在平面直角坐标系xOy中,直线l:![]() 交x轴于点M,
交x轴于点M,![]() 的半径为4,矩形ABCD沿直线运动
的半径为4,矩形ABCD沿直线运动![]() 在直线l上
在直线l上![]() ,
,![]() ,
,![]() 轴,当矩形ABCD是
轴,当矩形ABCD是![]() 的“随从矩形”时,点A的坐标为______.
的“随从矩形”时,点A的坐标为______.

【答案】(![]() )或(
)或(![]() )
)
【解析】
设直线l交![]() 于E、
于E、![]() 根据
根据![]() 的“随从矩形”的定义可知,当矩形ABCD的对角线的交点K与E或F重合时,四边形ABCD是
的“随从矩形”的定义可知,当矩形ABCD的对角线的交点K与E或F重合时,四边形ABCD是![]() 的“随从矩形”,利用平移的性质解决问题即可;
的“随从矩形”,利用平移的性质解决问题即可;
设直线l:![]() 交y轴于N,则
交y轴于N,则![]() ,
,![]() .
.

![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
设直线l交![]() 于E、
于E、![]() 作
作![]() 轴于G.
轴于G.
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,同法可得
,同法可得![]()
连接AC交BD于K,易证![]() 是边长为2的等边三角形,易知点K向上平移
是边长为2的等边三角形,易知点K向上平移![]() 个单位,再向右平移1个单位得到点A.
个单位,再向右平移1个单位得到点A.
根据![]() 的“随从矩形”的定义可知,当矩形ABCD的对角线的交点K与E或F重合时,四边形ABCD是
的“随从矩形”的定义可知,当矩形ABCD的对角线的交点K与E或F重合时,四边形ABCD是![]() 的“随从矩形”,
的“随从矩形”,
![]() ,
,![]() ,
,
![]() 或
或![]() 时,四边形ABCD是
时,四边形ABCD是![]() 的“随从矩形”.
的“随从矩形”.
故答案为![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】观察下表中的每一组值:
名称组别 |
|
|
| 名称组别 |
|
|
|
第1组 | 3 |
|
| 第5组 | |||
第2组 | 5 |
|
|
|
|
| |
第3组 | 7 |
|
|
|
|
| |
第4组 | 8 |
|
| 第 |
(1)根据表中前四组![]() 、
、![]() 、
、![]() 值的变化规律,第5组中
值的变化规律,第5组中![]() ;
;![]() ;第
;第![]() 组中
组中![]() ;
;![]() ;
;![]() .
.
(2)试证明以表中每组![]() 、
、![]() 、
、![]() 为边的三角形都是直角三角形.
为边的三角形都是直角三角形.