题目内容
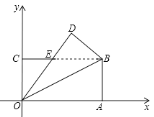
【题目】如图,矩形OABC的顶点与坐标原点O重合,将△OAB沿对角线OB所在的直线翻折,点A落在点D处,OD与BC相交于点E,已知OA=8,AB=4
(1)求证:△OBE是等腰三角形;
(2)求E点的坐标;
(3)坐标平面内是否存在一点P,使得以B,D,E,P为顶点的四边形是平行四边形?若存在,请直接写出P点坐标;若不存在,请说明理由.
【答案】(1)见解析; (2)(3,4); (3)(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)由矩形的性质得出OA∥BC,∠AOB=∠OBC,
由折叠的性质得∠AOB=∠DOB,得出∠OBC=∠DOB,证出OE=BE即可;
(2)设OE=BE=x,则CE=8-x,在Rt△OCE中,由勾股定理得出方程,解方程即可;
(3)先求出点D的坐标,然后根据B、D、E三点的坐标利用中点坐标公式分三种情况,即可求出P点的坐标.[点(a,b)与(c,d)所连线段的中点坐标是(![]() ,
,![]() )]
)]
解:
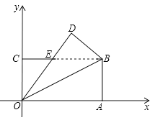
(1)证明:∵四边形OABC是矩形,
∴OA∥BC,
∴∠AOB=∠OBC,
由折叠的性质得:∠AOB=∠DOB,
∴∠OBC=∠DOB,
∴OE=BE,
∴△OBE是等腰三角形;
(2)设OE=BE=x,则CE=BC-BE=OA-BE=8-x,
在Rt△OCE中,由勾股定理得:42+(8-x)2=x2,
解得:x=5,
∴CE=8-x=3,
∵OC=4,
∴E点的坐标为(3,4);
(3)坐标平面内存在一点P,使得以B,D,E,P为顶点的四边形是平行四边形。理由如下:
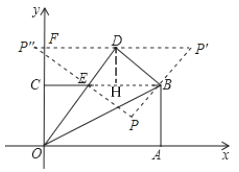
作DH⊥BE于H
在Rt△BDE中,BE=5,BD=4,DE=3
∴![]()
∴DH=![]()
∴EH=![]()
∴CH=![]()
∴点D的坐标是(![]() ,
,![]() )
)
∴当BE为平行四边形的对角线时,点P的坐标为(3+8-![]() ,4+4-
,4+4-![]() ),即(
),即(![]() ,
,![]() );
);
当BD为平行四边形的对角线时,点P的坐标为(8+![]() -3,4+
-3,4+![]() -4),即(
-4),即(![]() ,
,![]() );
);
当DE为平行四边形的对角线时,点P的坐标为(3+![]() -8,4+
-8,4+![]() -4),即(
-4),即(![]() ,
,![]() );
);
综上所述,坐标平面内存在一点P,使得以B,D,E,P为顶点的四边形是平行四边形,P点坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).