��Ŀ����
����Ŀ��������A��B��C�����Ӧ����a��b��c����(a+40)2+|b+10|��0��BΪ�߶�AC���е�.

(1)ֱ��д��A��B��C��Ӧ����a��b��c��ֵ.
(2)��ͼ1����D��ʾ����Ϊ10����P��Q�ֱ��A��Dͬʱ�������������˶�����P���ٶ�Ϊ6����λ/�룬��Q���ٶ�Ϊ1����λ/��.����P�˶���C��Ѹ����ԭ�ٷ��ص�A���۷���C���˶�����Q�˶���B���ֹͣ�˶���ͬʱP��Ҳֹͣ�˶�.���ڴ��˶�������P��Q�����������������϶�Ӧ����.
(3)��ͼ2��M��NΪA��C֮������(��M��N��ߣ������Dz���A��C�غ�)��E��F�ֱ�ΪAN��CM���е㣬��![]() ��ֵ.
��ֵ.
���𰸡�(1)a����40��b����10��c=20��(2)P��Q�����������������϶�Ӧ����Ϊ��4��![]() ��(3)
��(3)![]() =2.
=2.
��������
(1)����(a+40)2+|b+10|��0�������a��b��ֵ��BΪ�߶�AC���е�.���������c��ֵ��
(2)������������н��һ������A��D֮���״����������ǵ�P��C����Q���������˶�ʱ�䣬����������������������ϵ�з������ʱ�䣬���������Ӧʱ����Ӧ������
(3)�����߶ε��е�����壬���е��߶�EF��ʾAC�ɵó���.
�⣺(1)��(a+40)2+|b+10|��0��
��a����40��b����10��
��BΪ�߶�AC���е㣬
��![]() ����10��
����10��
��c��20��
����a����40��b����10��c��20��
(2)��ͼ1�����˶���ʱ��Ϊt�룬
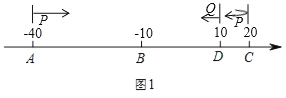
����P��Q��һ������ʱ����6t+t��10��(��40)��
��ã�t��![]() ��
��
��ʱ�������Ӧ����Ϊ10��![]() ��
��![]() ��
��
������P��C�����ϵ�Qʱ����6t��60��t+10��
��ã�t��14��
��ʱ�������Ӧ����Ϊ10��14����4��
���ڴ��˶�������P��Q�����������������϶�Ӧ����Ϊ��4��![]() ��
��
(3)��ͼ2����E��F�ֱ�ΪAN��CM���е㣬
��AN��2EN��CM��2MF��
��AC��2EN+2MF��MN
��![]() ��
��![]() ��
��![]() ��
��![]() ��2��
��2��
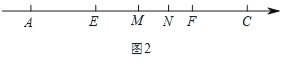

 ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�