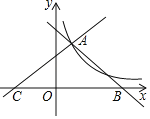
题目内容
【题目】如图,在平面直角坐标系中,直线![]() 交坐标轴于
交坐标轴于![]() 、
、![]() 点,点
点,点![]() 在线段
在线段![]() 上,以
上,以![]() 为一边在第一象限作正方形
为一边在第一象限作正方形![]() .若双曲线
.若双曲线![]() 经过点
经过点![]() ,
,![]() .则
.则![]() 的值为__________.
的值为__________.

【答案】8
【解析】
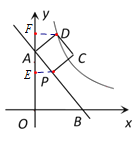
作PE⊥OA于E,作DF⊥OA于F.通过证明△EAP≌△FDA,可得DF=AE,AF=PE.根据勾股定理求出AE的长,进而求出点D的坐标,即可求出k的值.
作PE⊥OA于E,作DF⊥OA于F.
∵四边形APCD是正方形,
∴AP=AD=CD=2, ∠PAD=90°.
∵∠EAP+∠DAF=90°, ∠ADF+∠DAF=90°,
∴∠EAP=∠ADF.
在△EAP和△FDA中,
∵∠EAP=∠ADF,
∠AEP=∠AFD=90°,
AP=AD,
∴△EAP≌△FDA,
∴DF=AE,AF=PE.
∵![]() ,
,
∴AF=PE=![]() ,
,
∴AE=![]() =
=![]() ,
,
∴OF=![]() +
+![]() +
+![]() =5,
=5,
∴DF=![]() ,
,
∴D(![]() ,5),
,5),
∴k=![]() ×5=8.
×5=8.
故答案为:8.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目