题目内容
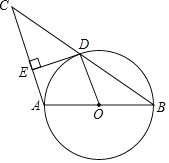
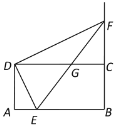
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 边上,与点
边上,与点![]() 、
、![]() 不重合,过点
不重合,过点![]() 作
作![]() 的垂线与
的垂线与![]() 的延长线相交于点
的延长线相交于点![]() ,连结
,连结![]() ,交
,交![]() 于点
于点![]() .
.
(1)当![]() 为
为![]() 的中点时,求
的中点时,求![]() 的长;
的长;
(2)当![]() 是以
是以![]() 为腰的等腰三角形时,求
为腰的等腰三角形时,求![]() .
.
【答案】(1)4;(2)![]() 或
或![]()
【解析】
(1)利用垂线性质,根据同角的余角相等可得到![]() ,证明
,证明![]() ∽
∽![]() ,利用对应边成比例,可得出AE的长;
,利用对应边成比例,可得出AE的长;
(2)分DE=DG时和ED=EG时两种情况,分别求出tan∠ADE的值.
解:(1)∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∴![]() .
.
又∵CD//AB,点G为EF的中点,
∴点C为BF的中点,
∴![]() ,
,
∴![]() ,∴
,∴![]() ;
;
(2)①当DE=DG时,则![]() ,
,
又∵CD//AB,
∴![]() ,
,
∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
在RtΔDAE中,![]() ,
,
∴![]() ,
,
解得![]() ,即
,即![]() ,
,
∴![]() ;
;
②当ED=EG时,![]() ,
,
又∵CD//AB,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
解得:![]() (舍去),
(舍去),
∴![]() ,
,
综上所述:![]() 或
或![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目