题目内容
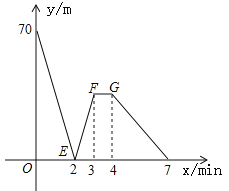
【题目】随着新冠肺炎的爆发,市场对口罩的需求量急剧增大.某口罩生产商自二月份以来,--直积极恢复产能,每日口罩生产量![]() (百万个)与天数
(百万个)与天数![]() 且
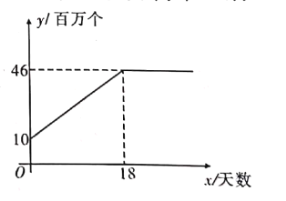
且![]() 为整数)的函数关系图象如图所示,而该生产商对口供应市场对口罩的需求量<(百万个)与天数
为整数)的函数关系图象如图所示,而该生产商对口供应市场对口罩的需求量<(百万个)与天数![]() 呈抛物线型,第
呈抛物线型,第![]() 天市场口罩缺口(需求量与供应量差)就达到
天市场口罩缺口(需求量与供应量差)就达到![]() (百万个),之后若干天,市场口罩需求量不断上升,在第
(百万个),之后若干天,市场口罩需求量不断上升,在第![]() 天需求量达到最高峰
天需求量达到最高峰![]() (百万个).
(百万个).
![]() 求出
求出![]() 与
与![]() 的函数解析式;
的函数解析式;
![]() 当市场供应量不小于需求量时,市民买口罩才无需提前预约,那么在整个二月份,市民无需预约即可购买口罩的天数共有多少天?
当市场供应量不小于需求量时,市民买口罩才无需提前预约,那么在整个二月份,市民无需预约即可购买口罩的天数共有多少天?
【答案】(1)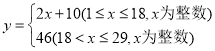 ;(2)在整个二月份,市民无需预约即可购买到口罩的天数共有
;(2)在整个二月份,市民无需预约即可购买到口罩的天数共有![]() 天.
天.
【解析】
(1)根据函数图象,结合待定系数法分段求解即可;
(2)根据题意设出抛物线顶点式,求出第一天口罩需求量,进而求出抛物线解析式,然后根据一次函数及二次函数的性质解答即可.
解:(1)当![]() 时,设
时,设![]() ,
,
把![]() ,
,![]() 代入,得
代入,得![]() ,解得
,解得![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]() ,
,
综上所述,![]() ;
;
![]() 由题意可设该生产商对口供应市场对口罩的需求量
由题意可设该生产商对口供应市场对口罩的需求量![]() ,
,
当![]() 时,代入
时,代入![]() 得
得![]() ,
,
此时口罩需求量为![]() (百万个),
(百万个),
将![]() 代入
代入![]() 中,得
中,得![]() ,
,
解得:![]() ,
,
所以![]() ,
,
当![]() 时,令
时,令![]() ,即
,即![]() ,
,
解得:![]() (舍去),
(舍去),![]() ,即此时需求和供应平衡,均为
,即此时需求和供应平衡,均为![]() 百万个,
百万个,
当![]() 时,
时,![]() 随着
随着![]() 增大而增大,
增大而增大,
故![]() ;
;
当![]() 时,
时,![]() ;
;
且当![]() 时,
时,![]() 随着
随着![]() 增大而减小,
增大而减小,
所以![]() ,
,
综上所述,从第![]() 天开始,
天开始,![]() ,
,
![]() (天),
(天),
答:在整个二月份,市民无需预约即可购买到口罩的天数共有![]() 天.
天.

【题目】某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的初三(1)班、(2)班进行了检测,如图表示从两班各随机抽取的10名学生的得分情况.
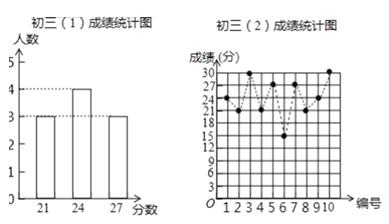
(1)利用图中提供的信息,补全下表:
班级 | 平均数/分 | 中位数/分 | 众数/分 | 方差/分 |
初三(1)班 | 24 | 24 | ________ | 5.4 |
初三(2)班 | 24 | _________ | 21 | ________ |
(2)哪个班的学生纠错的得分更稳定?若把24分以上(含24分)记为“优秀”,两班各40名学生,请估计两班各有多少名学生成绩优秀;
(3)现从两个班抽取了数学成绩最好的甲、乙、丙、丁四位同学,并随机分成两组进行数学竞赛,求恰好选中甲、乙一组的概率.