题目内容
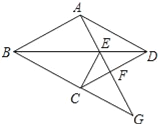
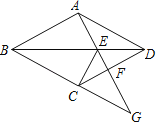
【题目】如图,四边形ABCD是菱形,点G是BC延长线上一点,连结AG,分别交BD、CD于点E、F,连结CE.
(1)求证:∠DAE=∠DCE;
(2)当CE=2EF时,EG与EF的等量关系是 .
【答案】(1)证明见解析;(2)FG=3EF.理由见解析.
【解析】(1)证明:∵四边形ABCD是菱形,
∴AD=CD,∠ADE=∠CDB;
在△ADE和△CDE中,
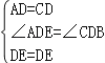
∴△ADE≌△CDE,
∴∠DAE=∠DCE.
 (2)解:结论:FG=3EF.
(2)解:结论:FG=3EF.
理由:∵四边形ABCD是菱形,
∴AD∥BC,
∴∠DAE=∠G,
由题意知:△ADE≌△CDE
∴∠DAE=∠DCE,
则∠DCE=∠G,
∵∠CEF=∠GEC,
∴△ECF∽△EGC,
∴![]() =
=![]() ,
,
∵EC=2EF,
∴![]() =
=![]() ,
,
∴EG=2EC=4EF,
∴FG=EG﹣EF=4EF﹣EF=3EF.

练习册系列答案
相关题目