题目内容
【题目】 推理填空
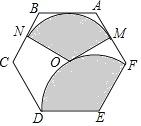
已知：如图所示，点B，C，E在同一条直线上，AB∥CD，∠1=∠2，∠3=∠4，求证：AD∥BE
证明：∵AB∥CD（已知）
∴∠4=∠______（______）
∵∠3=∠4（已知）∴∠3=∠______（______）
∴∠1=∠2（已知）∴∠1+∠CAF=∠2+∠CAF（等式的性质）
即∠BAF=∠DAC
∴∠3=∠______（等量代换）
∴AD∥BE（______）
【答案】BAE；两直线平行，同位角相等；BAE；等量代换；DAC；内错角相等，两直线平行．
【解析】
根据已知条件和解题思路，利用平行线的性质和判定填空．
解：AD∥BE，理由如下：
∵AB∥CD（已知），
∴∠4=∠BAE（两直线平行，同位角相等）；
∵∠3=∠4（已知），
∴∠3=∠BAE（等量代换）；
∵∠1=∠2（已知），
∴∠1+∠CAF=∠2+∠CAF（等式的性质），
即∠BAF=∠DAC，
∴∠3=∠DAC（等量代换），
∴AD∥BE（内错角相等，两直线平行）．
故答案为：BAE；两直线平行，同位角相等；BAE；等量代换；DAC；内错角相等，两直线平行．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
