��Ŀ����
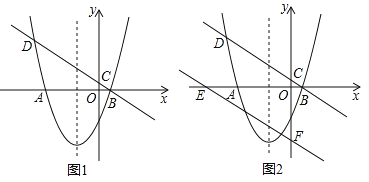
����Ŀ����ͼ1��������y=ax2+2x+c��x�ύ��A����4��0����B��1��0�����㣬����B��ֱ��y=kx+![]() �ֱ���y�ἰ�����߽��ڵ�C��D��
�ֱ���y�ἰ�����߽��ڵ�C��D��
��1����ֱ�ߺ������ߵı���ʽ��
��2������P�ӵ�O��������x��ĸ���������ÿ��1����λ���ȵ��ٶ����������˶������˶�ʱ��Ϊt�룬��tΪ��ֵʱ����PDCΪֱ�������Σ���ֱ��д����������������t��ֵ��
��3����ͼ2����ֱ��BD��y������ƽ��4����λ����x�ᣬy��ֱ���E��F���㣬�������ߵĶԳ������Ƿ���ڵ�M����ֱ��EF���Ƿ���ڵ�N��ʹDM+MN��ֵ��С�������ڣ��������Сֵ����M��N�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1�������߽���ʽΪ��y=![]() ��BD����ʽΪy=��
��BD����ʽΪy=��![]() ����2��t��ֵΪ
����2��t��ֵΪ![]() ��
��![]() ��
��![]() ����3��N����������2����2����M����������
����3��N����������2����2����M����������![]() ����
����![]() ����
����![]() .
.
����������1�����ô���ϵ�������ɵã�
��2������õ�D�����꣬����D�ֱ���DE��x�ᡢDF��y�ᣬ��P1D��P1C��P2D��DC��P3C��DC����������������������ε�������һ���ɵã�
��3��ͨ�����ԳƵ㣬������ת�����������룬Ӧ������֮���߶���̣�
��1����A����4��0����B��1��0������y=ax2+2x+c��
��![]() ��
��
��ã�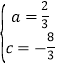 ��
��
�������߽���ʽΪ��y=![]() ��
��
�߹���B��ֱ��y=kx+![]() ��
��
����루1��0�����ã�k=��![]() ��
��
��BD����ʽΪy=��![]() ��
��
��2����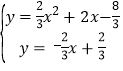 �ý�������ΪD����5��4����
�ý�������ΪD����5��4����
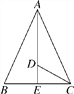
��ͼ1����D��DE��x���ڵ�E����DF��y���ڵ�F��
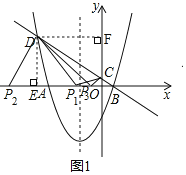
��P1D��P1Cʱ����P1DCΪֱ�������Σ�
����DEP1�ס�P1OC��
��![]() =
=![]() ����
����![]() =
=![]() ��
��
���t=![]() ��
��
��P2D��DC�ڵ�Dʱ����P2DCΪֱ��������
����P2DB�ס�DEB��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��ã�t=![]() ��
��
��P3C��DCʱ����DFC�ס�COP3��
��![]() =
=![]() ����
����![]() =
=![]() ��
��
��ã�t=![]() ��
��
��t��ֵΪ![]() ��
��![]() ��
��![]() ��
��
��3������ֱ֪��EF����ʽΪ��y=��![]() x��
x��![]() ��
��
����������ȡ��D�ĶԳƵ�D��������D����D��N��EF�ڵ�N���������߶Գ����ڵ�M
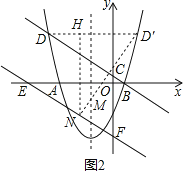
����N��NH��DD���ڵ�H����ʱ��DM+MN=D��N��С��
����EOF�ס�NHD��
���N������a����![]() ����
����
��![]() =
=![]() ����
����![]() =
=![]() ��
��
��ã�a=��2��
��N����������2����2����
���ֱ��ND���Ľ���ʽΪy=![]() x+1��
x+1��
��x=��![]() ʱ��y=��
ʱ��y=��![]() ��
��
��M����������![]() ����
����![]() ����
����
��ʱ��DM+MN��ֵ��СΪ![]() =
=![]() =2
=2![]() ��
��

 ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д�
ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д� â���̸����������������ϵ�д�
â���̸����������������ϵ�д�