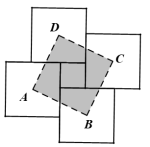
��Ŀ����
����Ŀ����ͼ����ʾ����֪������ABCD��������AEFG��G��A��B��ͬһֱ���ϣ���E��AD�ϣ�����DG��BE��
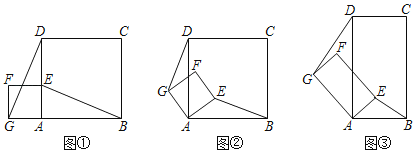
��1��֤����BE��DG��
��2�����֣���������AEFG�Ƶ�A��ת����ͼ����ʾ���ж�BE��DG��������ϵ��λ�ù�ϵ����˵�����ɣ�
��3��̽������ͼ����ʾ�����ı���ABCD���ı���AEFG��Ϊ���Σ���AD��2AB��AG��2AEʱ���ж�BE��DG��������ϵ��λ�ù�ϵ�Ƿ��루2���Ľ�����ͬ����˵�����ɣ�
���𰸡���1��֤������������2��BE��DG��BE��DG�����ɼ���������3��������ϵ��������BE��DG��DG��2BE�����ɼ�������λ�ù�ϵ���������ɼ�����
��������
��1�����������ε����ʼ�ȫ�������ε��ж��ɵ���ABE�ա�DAG��SAS�����ٸ���ȫ�������ε����ʼ��ɵó����ۣ�
��2�����������ε����ʿ�֪��AE��AG��AB��AD����BAD����EAG��90�����ٸ���ͬ�ŵ������ȵó���BAE����DAG��Ȼ�����ȫ�������ε��ж������ó���ABE�ա�DAG��SAS������ȫ�������ε����ʶ����ɵó�BE��DG����ABE����ADG���ӳ�BE��AD��T����DG��H�������ó���DHB=90�㣬��BE��DG��
��3�������ı���ABCD���ı���AEFG���Ǿ��Σ���AD��2AB��AG��2AEʱ������ABE�ס�ADG���ٸ������������ε����ʼ��ɵó����ۣ�
�⣺��1��֤�������ı���ABCD���ı���AEFG�������Σ�
��AE��AG��AB��AD����BAD����EAG��90����
���ABE�ա�DAG��SAS����
��BE��DG��
��2��BE��DG��BE��DG��
��ͼ1�У����ı���ABCD���ı���AEFG�������Σ�
��AE��AG��AB��AD����BAD����EAG��90����
���BAE����DAG��
����ABE����DAG��
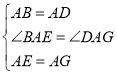 ��
��
���ABE�ա�DAG��SAS����
��BE��DG����ABE����ADG��
�ӳ�BE��AD��T����DG��H��

�ߡ�ATB+��ABE��90����
���ATB+��ADG��90����
�ߡ�ATB����DTH��
���DTH+��ADG��90����
���DHB��90����
��BE��DG��
��3��������ϵ�����������ǵ�������ϵΪDG��2BE��λ�ù�ϵ������
��ͼ2�У��ӳ�BE��AD��T����DG��H��
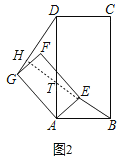
���ı���ABCD���ı���AEFG��Ϊ���Σ�
���BAD����DAG��
���BAE����DAG��
��AD��2AB��AG��2AE��
��![]() ��
��
���ABE�ס�ADG��
���ABE����ADG��![]() ��
��
��DG��2BE��
�ߡ�ATB+��ABE��90����
���ATB+��ADG��90����
�ߡ�ATB����DTH��
���DTH+��ADG��90����
���DHB��90����
��BE��DG��