题目内容
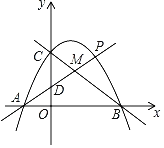
【题目】已知:在⊙O中,直径AB=4,点P、Q均在⊙O上,且∠BAP=60°,∠BAQ=30°,则弦PQ的长为_____.
【答案】2或4
【解析】
当点P和Q在AB的同侧,如图1,连接OP、OQ、PQ,先计算出∠PAQ=30°,根据圆周角定理得到∠POQ=60°,则可判断△OPQ为等边三角形,从而得到PQ=OP=2;当点P和Q在AB的同侧,如图1,连接PQ,先计算出∠PAQ=90°,根据圆周角定理得到PQ为直径,从而得到PQ=4.
解:当点P和Q在AB的同侧,如图1,连接OP、OQ、PQ,
∵∠BAP=60°,∠BAQ=30°,
∴∠PAQ=30°,
∴∠POQ=2∠PAQ=2×30°=60°,
∴△OPQ为等边三角形,
∴PQ=OP=2;
当点P和Q在AB的同侧,如图1,连接PQ,
∵∠BAP=60°,∠BAQ=30°,
∴∠PAQ=90°,
∴PQ为直径,
∴PQ=4,
综上所述,PQ的长为2或4.
故答案为2或4.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目