题目内容
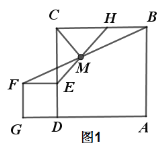
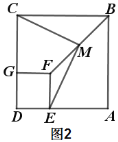
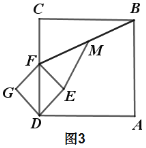
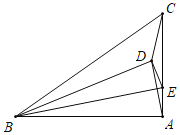
【题目】如图,在![]() 中,
中,![]() 点E为
点E为![]() 上的任意一点,连接
上的任意一点,连接![]() ,将
,将![]() 沿BE折叠,使点A落在点D处,连接
沿BE折叠,使点A落在点D处,连接![]() ,若
,若![]() 是直角三角形,则
是直角三角形,则![]() 的长为__________.
的长为__________.
【答案】![]()
【解析】
如图,由题意只有∠ACD可能为90°.过点B作BT⊥CD交CD的延长线于T.由翻折可知:BD=AB=8,AE=DE,设AE=DE=x,则EC=6x,由△BTD∽△DCE,可得CD=![]() ,在Rt△CDE中,根据DE=CD+EC,构建方程求出x即可解决问题.
,在Rt△CDE中,根据DE=CD+EC,构建方程求出x即可解决问题.
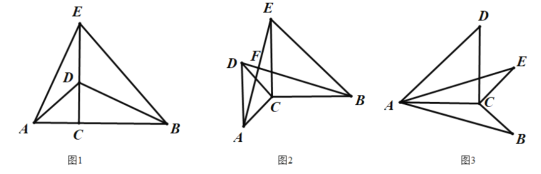
解:如图,由题意只有∠ACD可能为90°.过点B作BT⊥CD交CD的延长线于T.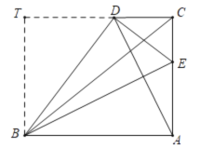
由翻折可知:BD=AB=8,AE=DE,
设AE=DE=x,则EC=6x,
∵∠T=∠DCE=∠BDE=∠BAC=90°,
∴四边形ABTC是矩形,
∴BT=AC=6,
∵∠BDT+∠TBD=90°,∠BDT+∠CDE=90°,
∴∠TBD=∠CDE,
∴△BTD∽△DCE,
∴![]() ,
,
∴![]() ,
,
∴CD=![]() ,
,
在Rt△CDE中,DE=CD+EC,
∴![]()
解得x=![]() 或
或![]() (舍去)
(舍去)
∴AE=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目