题目内容
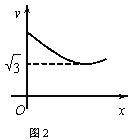
【题目】如图1，在等边△ABC中，D是BC的中点，P为AB 边上的一个动点，设AP=x，图1中线段DP的长为y，若表示y与x的函数关系的图象如图2所示，则△ABC的面积为（ ）
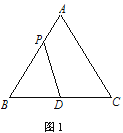
A. 4 B. 
C. 12 D. 
【答案】D
【解析】
由图1、图2结合题意可知，当DP⊥AB时，DP最短，由此可得DP最短=y最小=
，这样如图3，过点P作PD⊥AB于点P，连接AD，结合△ABC是等边三角形和点D是BC边的中点进行分析解答即可.
由题意可知：当DP⊥AB时，DP最短，由此可得DP最短=y最小=，如图3，过点P作PD⊥AB于点P，连接AD，
∵△ABC是等边三角形，点D是BC边上的中点，
∴∠ABC=60°，AD⊥BC，
∵DP⊥AB于点P，此时DP=，
∴BD=
，
∴BC=2BD=4，
∴AB=4，
∴AD=AB·sin∠B=4×sin60°=
，
∴S△ABC=
AD·BC=
.
故选D.
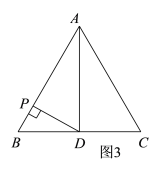
练习册系列答案
相关题目
【题目】某公司10名销售员，去年完成的销售额情况如表：
销售额（单位：万元） | 3 | 4 | 5 | 6 | 7 | 8 | 10 |
销售员人数（单位：人） | 1 | 3 | 2 | 1 | 1 | 1 | 1 |
（1）求销售额的平均数、众数、中位数；
（2）今年公司为了调动员工积极性，提高年销售额，准备采取超额有奖的措施，请根据（1）的结果，通过比较，合理确定今年每个销售员统一的销售额标准是多少万元？
