题目内容
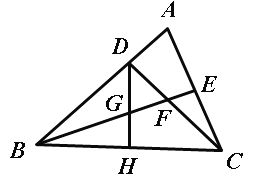
【题目】(1)如图1,在矩形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,过点
,过点![]() 作直线
作直线![]() ,且交
,且交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,且
,且![]() 平分
平分![]() .
.
①求证:四边形![]() 是菱形;
是菱形;
②直接写出![]() 的度数;
的度数;

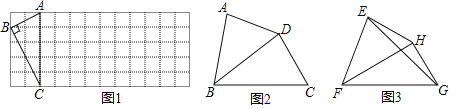
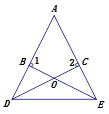
(2)把(1)中菱形![]() 进行分离研究,如图2,
进行分离研究,如图2,![]() 分别在
分别在![]() 边上,且
边上,且![]() ,连接
,连接![]() 为
为![]() 的中点,连接
的中点,连接![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .试探究线段
.试探究线段![]() 与
与![]() 之间满足的关系,并说明理由;
之间满足的关系,并说明理由;
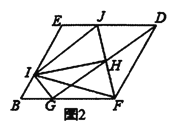
(3)把(1)中矩形![]() 进行特殊化探究,如图3,矩形
进行特殊化探究,如图3,矩形![]() 满足
满足![]() 时,点
时,点![]() 是对角线
是对角线![]() 上一点,连接
上一点,连接![]() ,作
,作![]() ,垂足为点
,垂足为点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() .请直接写出线段
.请直接写出线段![]() 三者之间满足的数量关系.
三者之间满足的数量关系.

【答案】(1)①见解析;②60°;(2)见解析;(3)见解析.
【解析】
(1)①由△DOE≌△BOF,推出EO=OF,由OB=OD,推出四边形EBFD是平行四边形,再证明EB=ED即可;②先证明∠ABD=2∠ADB,推出∠ADB=30°,即可解决问题;
(2)延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() ,由菱形性质,
,由菱形性质,![]() ,得
,得![]() ,由此
,由此![]() ,由ASA可证得
,由ASA可证得![]() ,由此
,由此![]() ,故
,故
![]() ,由
,由![]() ,可证得
,可证得![]() 是等边三角形,可得
是等边三角形,可得![]() ,
,![]() ,由SAS可证
,由SAS可证![]() ,可得
,可得![]() ,即
,即![]() 是等边三角形,
是等边三角形,
在![]() 中,由
中,由![]() ,
,![]() ,可得
,可得![]() ,由此可得
,由此可得![]() ;
;
(3)结论:EG2=AG2+CE2.如图3中,将△ADG绕点D逆时针旋转90°得到△DCM,先证明△DEG≌△DEM,再证明△ECM是直角三角形即可解决问题.
(1)①证明:如图1中,
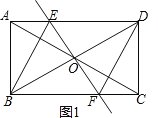
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() ,
,
∴![]() ,
,
∴四边形![]() 是菱形.
是菱形.
②∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() =
=![]() ,
,
∵四边形![]() 是矩形,
是矩形,
∴![]() A=
A=![]() ,
,
∴![]() +
+![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴![]() ;
;
(2)结论:![]() .
.
理由:如图2中,延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() .
.

∵四边形![]() 是菱形,
是菱形,![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]()
在![]() 和
和![]() 中,
中,
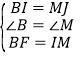 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
在![]() 中,∵
中,∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)结论:![]() .
.
理由:如图3中,将△ADG绕点D逆时针旋转90°得到△DCM,

∵∠FAD+∠DEF=90°,
∴AFED四点共圆,
∴∠EDF=∠DAE=45°,∠ADC=90°,
∴∠ADF+∠EDC=45°,
∵∠ADF=∠CDM,
∴∠CDM+∠CDE=45°=∠EDG,
在△DEM和△DEG中,
 ,
,
∴△DEG≌△DEM,
∴GE=EM,
∵∠DCM=∠DAG=∠ACD=45°,AG=CM,
∴∠ECM=90°,
∴EC2+CM2=EM2,
∵EG=EM,AG=CM,
∴GE2=AG2+CE2.

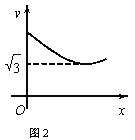
【题目】在《科学》课上,老师讲到温度计的使用方法及液体的沸点时,好奇的王红同学准备测量食用油的沸点,已知食用油的沸点温度高于水的沸点温度(![]() ),王红家只有刻度不超过
),王红家只有刻度不超过![]() 的温度计,她的方法是在锅中倒入一些食用油,用煤气灶均匀加热,并每隔
的温度计,她的方法是在锅中倒入一些食用油,用煤气灶均匀加热,并每隔![]() 测量一次锅中油温,测量得到的数据如下表:
测量一次锅中油温,测量得到的数据如下表:
时间 | 0 | 10 | 20 | 30 | 40 |
油温 | 10 | 30 | 50 | 70 | 90 |
王红发现,烧了![]() 时,油沸腾了,则下列说法不正确的是( )
时,油沸腾了,则下列说法不正确的是( )
A. 没有加热时,油的温度是![]()
B. 加热![]() ,油的温度是
,油的温度是![]()
C. 估计这种食用油的沸点温度约是![]()
D. 每加热![]() ,油的温度升高
,油的温度升高![]()