题目内容
【题目】(1)解方程:x2﹣5=4x.
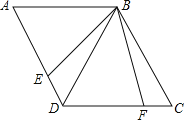
(2)如图,四边形ABCD中,∠C=60°,∠BED=110°,BD=BC,点E在AD上,将BE绕点B逆时针旋转60°得BF,且点F在DC上,求∠EBD的度数.
【答案】(1)x1=5,x2=﹣1;(2)∠EBD=10°.
【解析】
(1)利用因式分解法解方程即可;
(2)证明△BCD是等边三角形,得出∠DBC=60°,由旋转的性质得出∠EBF=60°,BE=BF,得出∠EBD=∠FBC,证明△BDE≌△BCF(SAS),得出∠BDE=∠C=60°,由三角形内角和定理即可得出答案.
解:(1)x2﹣5=4x;
原方程变形得:x2﹣4x﹣5=0,
因式分解得:(x﹣5)(x+1)=0,
于是得:x﹣5=0,或x+1=0,
∴x1=5,x2=﹣1;
(2)∵∠C=60°,BD=BC,
∴△BCD是等边三角形,
∴∠DBC=60°,
由旋转的性质得:∠EBF=60°,BE=BF,
∴∠EBD=∠FBC,
在△BDE和△BCF中,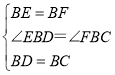 ,
,
∴△BDE≌△BCF(SAS),
∴∠BDE=∠C=60°,
∴∠EBD=180°﹣∠BED﹣∠BDE=180°﹣110°﹣60°=10°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
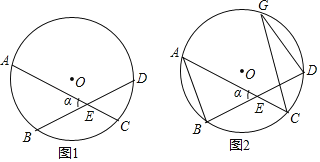
【题目】如图1,圆O的两条弦AC、BD交于点E,两条弦所成的锐角或者直角记为∠α
(1)点点同学通过画图和测量得到以下近似数据:
| 30.2° | 40.4° | 50.0° | 61.6° |
| 55.7° | 60.4° | 80.2° | 100.3° |
∠α的度数 | 43.0° | 50.2° | 65.0° | 81.0° |
猜想:![]() 、
、![]() 、∠α的度数之间的等量关系,并说明理由﹒
、∠α的度数之间的等量关系,并说明理由﹒
(2)如图2,若∠α=60°,AB=2,CD=1,将以![]() 圆心为中心顺时针旋转,直至点A与点D重合,同时B落在圆O上的点,连接CG﹒
圆心为中心顺时针旋转,直至点A与点D重合,同时B落在圆O上的点,连接CG﹒
①求弦CG的长;
②求圆O的半径.