题目内容
（1）计算：cos60°+sin245°-tan30°•tan45°；
（2）在Rt△ABC中，∠ACB=90°，CD⊥AB于D，AB=2BC，求cos∠ACD的值．
（2）在Rt△ABC中，∠ACB=90°，CD⊥AB于D，AB=2BC，求cos∠ACD的值．
（1）原式=
+（
）2-
×1
=
+
-
=1-
；
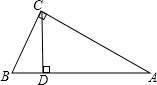
（2）∵∠ACB=90°，AB=2BC，
∴∠A=30°，
∵CD⊥AB，∴∠ACD=60°，
∴cos∠ACD=cos60°=
．
| 1 |
| 2 |
| ||
| 2 |
| ||
| 3 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
=1-
| ||
| 3 |
（2）∵∠ACB=90°，AB=2BC，
∴∠A=30°，
∵CD⊥AB，∴∠ACD=60°，
∴cos∠ACD=cos60°=
| 1 |
| 2 |
练习册系列答案
相关题目
高忽略不计，1步=0.8m，结果精确到1m）
