题目内容
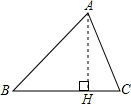
如图，在△ABC中，BC=9，AB=6
，∠ABC=45°．
（1）求△ABC的面积；
（2）求cos∠C的值．
| 2 |
（1）求△ABC的面积；
（2）求cos∠C的值．
（1）作AH⊥BC，H为垂足，（1分）
则在△ABH中，∠AHB=90°，∠B=45°，AB=6
，
∴AH=AB•sin45°=6，（2分）
∴S△ABC=
BC•AH=
×9×6=27．（2分）
（2）由（1）可知BH=AB•cos45°=6，（1分）
在△ACH中，∠AHC=90°，CH=BC-BH=3，AH=6，
则AC=
=3
，（2分）
∴cos∠C=
=
．（2分）
则在△ABH中，∠AHB=90°，∠B=45°，AB=6
| 2 |
∴AH=AB•sin45°=6，（2分）
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
（2）由（1）可知BH=AB•cos45°=6，（1分）
在△ACH中，∠AHC=90°，CH=BC-BH=3，AH=6，
则AC=
| AH2+CH2 |
| 5 |
∴cos∠C=
| CH |
| AC |
| ||
| 5 |
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
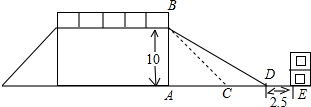原坡脚10米的建筑物是否需要拆除？请说明理由．（参考数据：