题目内容
如图①,正方形 的顶点
的顶点 的坐标分别为
的坐标分别为 ,顶点
,顶点 在第一象限.点
在第一象限.点 从点
从点 出发,沿正方形按逆时针方向匀速运动,同时,点
出发,沿正方形按逆时针方向匀速运动,同时,点 从点
从点 出发,沿
出发,沿 轴正方向以相同速度运动.当点
轴正方向以相同速度运动.当点 到达点
到达点 时,
时, 两点同时停止运动,设运动的时间为
两点同时停止运动,设运动的时间为 秒.
秒.

(1)求正方形 的边长.(2分)
的边长.(2分)
(2)当点 在
在 边上运动时,
边上运动时, 的面积
的面积 (平方单位)与时间
(平方单位)与时间 (秒)之间的函数图象为抛物线的一部分(如图②所示),求
(秒)之间的函数图象为抛物线的一部分(如图②所示),求 两点的运动速度.(2分)
两点的运动速度.(2分)
(3)求(2)中面积 (平方单位)与时间
(平方单位)与时间 (秒)的函数关系式及面积
(秒)的函数关系式及面积 取最大值时点
取最大值时点 的坐标.(4分)
的坐标.(4分)
(4)若点 保持(2)中的速度不变,则点
保持(2)中的速度不变,则点 沿着
沿着 边运动时,
边运动时, 的大小随着时间
的大小随着时间 的增大而增大;沿着
的增大而增大;沿着 边运动时,
边运动时, 的大小随着时间
的大小随着时间 的增大而减小.当点
的增大而减小.当点 沿着这两边运动时,使
沿着这两边运动时,使 的点
的点 有 个.(2分)
有 个.(2分)
(抛物线 的顶点坐标是
的顶点坐标是 .)
.)
 的顶点
的顶点 的坐标分别为
的坐标分别为 ,顶点
,顶点 在第一象限.点
在第一象限.点 从点
从点 出发,沿正方形按逆时针方向匀速运动,同时,点
出发,沿正方形按逆时针方向匀速运动,同时,点 从点
从点 出发,沿
出发,沿 轴正方向以相同速度运动.当点
轴正方向以相同速度运动.当点 到达点
到达点 时,
时, 两点同时停止运动,设运动的时间为
两点同时停止运动,设运动的时间为 秒.
秒.
(1)求正方形
 的边长.(2分)
的边长.(2分)(2)当点
 在
在 边上运动时,
边上运动时, 的面积
的面积 (平方单位)与时间
(平方单位)与时间 (秒)之间的函数图象为抛物线的一部分(如图②所示),求
(秒)之间的函数图象为抛物线的一部分(如图②所示),求 两点的运动速度.(2分)
两点的运动速度.(2分)(3)求(2)中面积
 (平方单位)与时间
(平方单位)与时间 (秒)的函数关系式及面积
(秒)的函数关系式及面积 取最大值时点
取最大值时点 的坐标.(4分)
的坐标.(4分)(4)若点
 保持(2)中的速度不变,则点
保持(2)中的速度不变,则点 沿着
沿着 边运动时,
边运动时, 的大小随着时间
的大小随着时间 的增大而增大;沿着
的增大而增大;沿着 边运动时,
边运动时, 的大小随着时间
的大小随着时间 的增大而减小.当点
的增大而减小.当点 沿着这两边运动时,使
沿着这两边运动时,使 的点
的点 有 个.(2分)
有 个.(2分)(抛物线
 的顶点坐标是
的顶点坐标是 .)
.)(1)10(2)每秒1个单位(3) ,
, (4)2
(4)2
 ,
, (4)2
(4)2(1)作 轴于
轴于 .
.
 ,
,
 .
.
 . (2分)
. (2分)
(2)由图②可知,点 从点
从点 运动到点
运动到点 用了10秒.
用了10秒.
又 .
.
 两点的运动速度均为每秒1个单位. (4分)
两点的运动速度均为每秒1个单位. (4分)
(3)方法一:作 轴于
轴于 ,则
,则 .
.
 ,即
,即 .
.
 .
.
 .
.
 ,
,
 . (6分)
. (6分)
即 .
.
 ,且
,且 ,
,
 当
当 时,
时, 有最大值.
有最大值.
此时 ,
,
 点
点 的坐标为
的坐标为 . (8分)
. (8分)
方法二:当 时,
时, .
.
设所求函数关系式为 .
.
 抛物线过点
抛物线过点 ,
,


 . (6分)
. (6分)
 ,且
,且 ,
,
 当
当 时,
时, 有最大值.
有最大值.
此时 ,
,
 点
点 的坐标为
的坐标为 . (8分)
. (8分)
(4) .
.
(1)本题须先作BF⊥y轴于F.再求出FB和FA的值即可得出AB的长.
(2)本题须求出点P从点A运动到点B用了多少时间,再根据AB的长即可求出P、Q两点的运动速度.
(3)本题须先作PG⊥y轴于G,证出△AGP∽△AFB得出S= OQ•OG,再把OQ•OG的值代入即可得出
OQ•OG,再把OQ•OG的值代入即可得出 最后即可得出S有最大值时P点的坐标.
最后即可得出S有最大值时P点的坐标.
(4)本题要分两种情况进行讨论:①P在AB上,②P在BC上
 轴于
轴于 .
. ,
, .
. . (2分)
. (2分)(2)由图②可知,点
 从点
从点 运动到点
运动到点 用了10秒.
用了10秒.又
 .
. 两点的运动速度均为每秒1个单位. (4分)
两点的运动速度均为每秒1个单位. (4分)(3)方法一:作
 轴于
轴于 ,则
,则 .
. ,即
,即 .
. .
. .
. ,
, . (6分)
. (6分)即
 .
. ,且
,且 ,
, 当
当 时,
时, 有最大值.
有最大值.此时
 ,
, 点
点 的坐标为
的坐标为 . (8分)
. (8分)方法二:当
 时,
时, .
.设所求函数关系式为
 .
. 抛物线过点
抛物线过点 ,
,

 . (6分)
. (6分) ,且
,且 ,
, 当
当 时,
时, 有最大值.
有最大值.此时
 ,
, 点
点 的坐标为
的坐标为 . (8分)
. (8分)(4)
 .
.(1)本题须先作BF⊥y轴于F.再求出FB和FA的值即可得出AB的长.
(2)本题须求出点P从点A运动到点B用了多少时间,再根据AB的长即可求出P、Q两点的运动速度.
(3)本题须先作PG⊥y轴于G,证出△AGP∽△AFB得出S=
 OQ•OG,再把OQ•OG的值代入即可得出
OQ•OG,再把OQ•OG的值代入即可得出 最后即可得出S有最大值时P点的坐标.
最后即可得出S有最大值时P点的坐标.(4)本题要分两种情况进行讨论:①P在AB上,②P在BC上

练习册系列答案
相关题目
 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).
 ,下列说法错误的是( )
,下列说法错误的是( ) 时,
时, 随
随 的增大而减小
的增大而减小
 时,不等式
时,不等式 的解集是
的解集是
 ,则
,则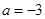
 与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3. (
( ≠0)的对称轴是直线
≠0)的对称轴是直线 =
=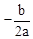

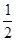 ;④在对称轴左侧,y随x增大而增大.其中正确有( )
;④在对称轴左侧,y随x增大而增大.其中正确有( ) 时,下列函数中,函数值
时,下列函数中,函数值 随自变量
随自变量 增大而增大的是 (只填写序号)
增大而增大的是 (只填写序号) ;②
;② ;③
;③ ;④
;④ .
. 的对称轴是直线
的对称轴是直线 ,且经过点
,且经过点 (3,0),则
(3,0),则 的值为( )
的值为( )
