题目内容
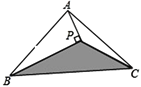
【题目】如图，半径均为整数的同心圆组成的“圆环带”，若大圆的弦AB与小圆相切于点P，且弦AB的长度为定值
， 则满足条件的不全等的“圆环带”有（ ）
A.1个
B.2个
C.3个
D.无数个
【答案】A
【解析】解：连结OP、OA，如图，
∵大圆的弦AB与小圆相切于点P，
∴OP⊥AB，
∴AP=BP=
AB=2
，
在Rt△OAP中，OA2﹣OP2=AP2=（2）2=12，
∴（OA﹣OP）（OA+OP）=12，
而OA、OP为整数，
∴
或
或
，
解得
，
∴满足条件的不全等的“圆环带”有1个，即大圆半径为4，小圆半径为2．
故选A．
【考点精析】本题主要考查了切线的性质定理的相关知识点，需要掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题．
练习册系列答案
备战中考寒假系列答案
相关题目
