题目内容
【题目】如图,在△ABC中,∠A=90°,AB=AC=2,点O是边BC的中点,半圆O与△ABC相切于点D、E,则阴影部分的面积等于( )
A.1﹣![]()
B.![]()
C.1﹣![]()
D.![]()
【答案】B
【解析】解:连接OD,OE,
∵半圆O与△ABC相切于点D、E,
∴OD⊥AB,OE⊥AC,
∵在△ABC中,∠A=90°,AB=AC=2,
∴四边形ADOE是正方形,△OBD和△OCE是等腰直角三角形,
∴OD=OE=AD=BD=AE=EC=1,
∴∠ABC=∠EOC=45°,
∴AB∥OE,
∴∠DBF=∠OEF,
在△BDF和△EOF中,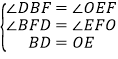 ,
,
∴△BDF≌△EOF(AAS),
∴S阴影=S扇形DOE=![]() ×π×12=
×π×12=![]() .
.
故选B.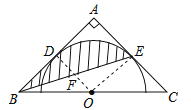
【考点精析】本题主要考查了切线的性质定理的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目