题目内容
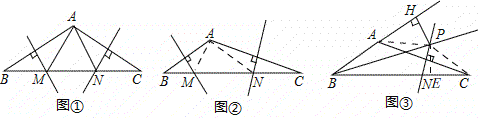
【题目】在△ABC中,AB、AC边的垂直平分线分别交BC边于点M、N.
(1)如图①,若△AMN是等边三角形,则∠BAC= °;
(2)如图②,若∠BAC=135°,求证:BM2+CN2=MN2.
(3)如图③,∠ABC的平分线BP和AC边的垂直平分线相交于点P,过点P作PH垂直BA的延长线于点H.若AB=4,CB=10,求AH的长.

【答案】1200
【解析】
(1)先求出∠AMN=60°,再利用垂直平分线求出∠B=30°,同理求出∠C=30°,最后利用三角形内角和定理即可得出结论;
(2)先判断出∠B+∠C=45°,进而求出∠MAN=90°,即可得出结论;
(3)先判断出Rt△APH≌Rt△CPE,进而判断出Rt△BPH≌Rt△BPE,即可得出结论.
解:(1)如图①,∵△AMN是等边三角形,
∴∠AMN=60°,
∵MG是AB的垂直平分线,
∴AM=AM,
∴∠B=∠BAM=30°
同理:∠C=30°,
∴∠BAC=180°-∠B-∠C=120°
故答案为120;
(2)如图①,连接AM、AN
∵∠BAC=135°
∴∠B+∠C=45°,
又∵点M在AB的垂直平分线上
∴AM=BM
∴∠BAM=∠B,
同理AN=CN,∠CAN=∠C
∴∠BAM+∠CAN=45°
∴∠MAN=90°,
∴AM2+AN2=MN2;
∴BM2+CN2=MN2;
(3)如图②,连接AP、CP,过点P作PE⊥BC于点E
∵BP平分∠ABC,PH⊥BA,PE⊥BC
∴PH=PE
∵点P在AC的垂直平分线上
∴AP=CP
在Rt△APH和Rt△CPE中
![]()
∴Rt△APH≌Rt△CPE
∴AH=CE,
∵BP平分∠ABC,PH⊥BA,PE⊥BC
∴∠HBP=∠CBP,∠BHP=∠BEP=90°
∵BP=BP
∴Rt△BPH≌Rt△BPE
∴BH=BE,
∴BC=BE+CE=BH+CE=AB+2AH
∴AH=(BC-AB)÷2=3.

【题目】我国有五座名山,但在洪雅人的心目中,我国有六座名山,这六座名山的海拔分别为:
山名 | 泰山 | 华山 | 黄山 | 庐山 | 峨嵋山 | 瓦屋山 |
海拔(米) | 1152 | 1997 | 1873 | 1500 | 1309 | 2830 |
(1)海拔最高的山是多少,最高的山与最低的山的海拔相差多少米;
(2)海拔不低于1500米的山的频数是多少;频率是多少;
(3)根据数据制作条形统计图.
【题目】为了解学生对安全知识的掌握情况,学校随机抽取了20名学生进行安全知识测试,测试成绩(百分制)如下:
78、86、93、81、97、88、79、93、87、90、93、98、88、81、94、95、81、98、99、94
(1)根据上述数据,将下列表格补充完整(每组含最小值):
成绩/分 | 70~80 | 80~90 | 90~100 |
人数 | 7 |
(2)若用(1)中数据制作扇形统计图,求出表示“70~80”扇形的圆心角度数;
(3)已知该校共有2000名学生,若规定成绩90分及以上为优秀,估计该校学生对安全知识掌握情况为优秀的有多少人?