题目内容
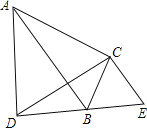
【题目】如图,在平行四边形ABCD中,将四边形折叠,使点A落在BC边上的点E处,折痕为BF.
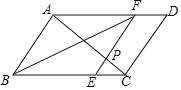
(1)求证:四边形ABEF为菱形;
(2)连接AC交EF于点P, 若CD=2CE,S△PCE=2,求![]() PAF的面积.
PAF的面积.
【答案】(1)见解析;(2)面积为8
【解析】
(1)依据条件可得AB=BE=AF=EF,即可得到四边形ABEF是菱形;
(2)首先求出AF=2CE,然后依据AF∥CE,可得△PCE∽△PAF,进而得出![]() =(
=(![]() )2=
)2=![]() ,即可求出结果.
,即可求出结果.
解:(1)如图,由折叠可知,AB=BE,AF=EF,∠1=∠2,
在平行四边形ABCD中,AD∥BC,即AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=AF,
∴AB=BE=AF=EF,
∴四边形ABEF是菱形;
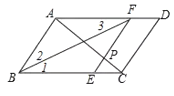
(2)在平行四边形ABCD中,CD=AB,
∵CD=2CE,AF=AB,
∴AF=2CE,
∵AF∥CE,
∴△PCE∽△PAF,
∴![]() =(
=(![]() )2=
)2=![]() ,
,
∴S△PAF=4×2=8.

练习册系列答案
相关题目