题目内容
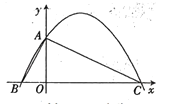
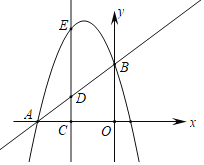
【题目】如图，已知直线y＝x+4交x轴于点A，交y轴于点B，抛物线y＝﹣x2+bx+c经过点A、B．
（1）求抛物线解析式；
（2）点C（m，0）是x轴上异于A、O点的一点，过点C作x轴的垂线交AB于点D，交抛物线于点E．
①当点E在直线AB上方的抛物线上时，连接AE、BE，求S△ABE的最大值；
②当DE＝AD时，求m的值．
【答案】（1）y＝﹣x2﹣3x+4；（2）①S△ABE最大值为8；②m＝
.
【解析】
（1）直线y＝x+4交x轴于点A，交y轴于点B，则点A、B的坐标分别为：（﹣4，0）、（0，4），可得c值，把A点坐标代入y＝﹣x2+bx+c求出b的值，即可得答案；（2）①S△ABE＝
×ED×OA＝2ED＝﹣2m2﹣8m，即可求解；②根据A、B坐标可得∠BAO=45°，即可得出AD＝
AC＝|（m+4）|，根据AD=DE列方程求出m的值即可．
（1）∵直线y＝x+4交x轴于点A，交y轴于点B，
∴当x=0时，y=4，当y=0时，x=-4，
∴点A（-4，0）、点B（0，4），
∴c＝4，
将点A的坐标代入抛物线表达式并解得：-(-4)2-4x+4=0，
解得：b＝﹣3，
故抛物线的表达式为：y＝﹣x2﹣3x+4；
（2）如图，连接EA、EB，
①∵C（m，0），CE⊥x轴，D、E分别在AB和抛物线上，
∴点E、D的坐标分别为：（m，﹣m2﹣3m+4）、（m，m+4），
∵点E在直线AB上方的抛物线上，
∴DE＝（﹣m2﹣3m+4）﹣（m+4）＝﹣m2﹣4m，
∴S△ABE＝×ED×OA＝2ED＝﹣2m2﹣8m=-2(m+2)2+8，
∵﹣2＜0，
∴当m=-2时，S△ABE有最大值8.
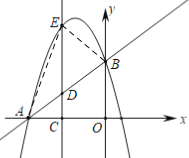
②∵OA=OB=4，∠AOB=90°，
∴∠BAO=45°，
∵∠ACE=90°，
∴AD＝AC＝|m+4|，
∵AD=DE，
∴
解得：m=或m=-4，
∵m=-4时，点C与点A重合，不符合题意，
∴m=.
