题目内容
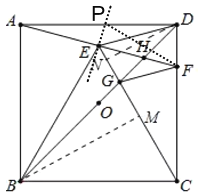
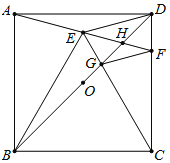
【题目】如图,正方形ABCD中, O为BD中点,以BC为边向正方形内作等边![]() BCE,连接并延长AE交CD于F,连接BD分别交CE,AF于G ,H ,下列结论:①∠CEH=45°;②GF//DE;③2OH+DH=BD;④BG=
BCE,连接并延长AE交CD于F,连接BD分别交CE,AF于G ,H ,下列结论:①∠CEH=45°;②GF//DE;③2OH+DH=BD;④BG=![]() DG;⑤
DG;⑤![]() △BEC : S△BGC=
△BEC : S△BGC=![]() .其中正确的结论是( )
.其中正确的结论是( )
A.①②⑤B.①②④C.①②D.②③④
【答案】A
【解析】
①根据正方形的性质及等边三角形的性质求出∠BAE=∠BEA=∠CED=∠CDE=75°,∠EAD=∠EDA=15°,然后可得∠CEH=45°.
②由条件可以得出∠BDE=30°,∠DEF=30°,然后证明△DEF≌△EDG,得出DF=EG,进而得出CG=CF,求出∠CGF=75°,由∠CED=75°,就可以得出GF∥DE;
③由O为BD中点可以得出,BD=2OD=2(OH+HD),BDDH=BH,得出BH=2(OH+HD)DH=2OH+DH;
④ 设AB=BC=CD=AD=x,推出BM=![]() x,DN=
x,DN=![]() x,由
x,由![]() 可得
可得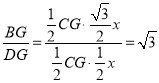 ,即可求出BG=
,即可求出BG=![]() DG.
DG.
⑤作AF的垂直平分线交AD于P,设DF=a,CE=BC=AD=![]() ,GE=DF=a,然后可得GC=
,GE=DF=a,然后可得GC=![]() ,由S△BEC:S△BGC=EC:CG,即可解决问题.
,由S△BEC:S△BGC=EC:CG,即可解决问题.
解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABC=∠BCD=∠CDA=∠DAB=90°,∠ADB=∠CDB=45°.
∵△BEC是等边三角形,
∴BC=BE=CE,∠EBC=∠BCE=∠BEC=60°,
∴AB=BE=CE=CD,∠ABE=∠DCE=30°,
∴∠BAE=∠BEA=∠CED=∠CDE=75°,
∴∠EAD=∠EDA=15°,
∴∠DEF=30°,
∴∠CEH=45°,故①正确;
∵∠EDC=75°,∠BDC=45°,
∴∠EDB=30°,
∴∠DEF=∠EDG,∠EGD=75°.
∵∠ADC=90°,∠DAF=15°,
∴∠EFD=75°,
∴∠EFD=∠EGD.
在△DEF和△EDG中,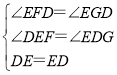 ,
,
∴△DEF≌△EDG,
∴DF=EG,
∵EC=DC,
∴ECEG=DCDF,
∴CG=CF,
∴∠CGF=∠CFG=75°,
∴∠CED=∠CGF,
∴GF∥DE,故②正确;
O为BD中点,
∴BD=2OD=2(OH+HD),
∵BDDH=BH,
∴BH=2(OH+HD)DH=2OH+2HDHD=2OH+DH.故③错误;
作BM⊥CG于M,DN⊥CE于N,
∴∠BMC=∠DNC=90°,
∴BM=sin60°BC,DN=sin30°CD,
设AB=BC=CD=AD=x,
∴BM=![]() ,DN=
,DN=![]() ,
,
∵![]() ,
,
∴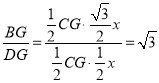 ,即BG=
,即BG=![]() DG,故④错误;
DG,故④错误;
⑤作AF的垂直平分线交AD于P,则∠DAF=∠AFP=15°,
∴∠DPF=30°,
设DF=a,
则PF=2a,DP=![]() ,
,
∴AP=PF=2a,
∴AD=![]() ,
,
∴CE=BC=AD=![]() ,GE=DF=a,
,GE=DF=a,
∴GC=![]() ,
,
∵S△BEC:S△BGC=EC:GC,
∴S△BEC:S△BGC=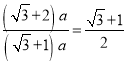 ,故⑤正确.
,故⑤正确.
综上所述,正确的是①②⑤,
故选:A.