题目内容
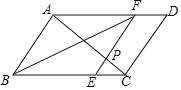
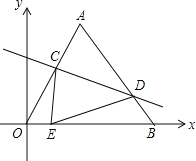
【题目】如图△ABC≌△DEC,公共顶点为C,B在DE上,则有结论①∠ACD=∠BCE=∠ABD;②∠DAC+∠DBC=180°;③△ADC∽△BEC;④CD⊥AB,其中成立的是( )
A.①②③B.只有②④C.只有①和②D.①②③④
【答案】A
【解析】
先根据全等三角形的性质,得到哪些等角和等边,然后根据这些等量条件来判断各结论是否正确.
解:∵△ABC≌△DEC,且C为公共顶点,
∴∠ABC=∠E,∠ACB=∠DCE,BC=CE;
由∠ACB=∠DCE,得∠ACD=∠BCE=∠ACB-∠BCD=∠DCE-∠BCD,
由BC=CE,得∠CBE=∠E,
∴∠ABC=∠CBE=∠E,∠ACD=∠BCE;
又∵∠ABD=180°-∠ABC-∠CBE,∠BCE=180°-∠CBE-∠E,
∴∠ABD=∠BCE=∠ACD,故①正确;
∵△ABC≌△DEC,且C为公共顶点,
∴AC=CD,即∠ACD=180°-2∠ADC;
又∵∠BCE=180°-2∠E,且∠ACD=∠BCE,
∴∠ADC=∠E=∠ABC;
由已知的全等三角形,还可得:∠BAC=∠BDC,
∴∠DAC+∠DBC=∠BAC+∠BAD+∠ABC+∠ABD=∠BAD+∠ADB+∠ABD=180°;
故②正确;
由②∠DAC+∠DBC=180°知,A、D、B、C四点共圆,
由圆周角定理知:∠ADC=∠ABC=∠E;
结合①②的证明过程知:△ADC、△BEC都是等腰三角形,且它们的底角相等,
故△ADC∽△BEC,③正确;
由于缺少条件,无法证明④的结论一定成立,故④错误;
所以正确的结论为①②③,
故选:A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目