题目内容
【题目】某工厂现有甲种原料360千克，乙种原料290千克，计划利用这两种原料生产A、B两种产品共50件，已知生产一件A种产品用甲种原料9千克，乙种原料3千克，可获利700元；生产一件B种产品用甲种原料4千克，乙种原料10千克，可获利1200元．
（1）按要求安排A、B两种产品的生产件数，有哪几种方案？请你设计出来；
（2）设生产A、B两种产品总利润为y元，其中一种产品生产件数为x件，试写出y与x之间的函数关系式，并利用函数的性质说明那种方案获利最大？最大利润是多少？
【答案】（1）①安排A种产品30件，B种产品20件；②安排A种产品31件，B种产品19件；③安排A种产品32件，B种产品18件；
（2）y=﹣500x+60000， A种产品30件，B种产品20件，对应方案的利润最大，最大利润为45000元。
【解析】分析：（1）本题首先找出题中的等量关系即甲种原料不超过360千克，乙种原料不超过290千克，然后列出不等式组并求出它的解集．由此可确定出具体方案．（2）根据题意列出y与x之间的函数关系式，利用一次函数的增减性和（1）得到的取值范围即可求得最大利润．
本题解析:
（1）设生产A种产品x件，那么B种产品（50﹣x）件，则：
，
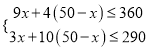解得：30≤x≤32，∵x为正整数，∴x=30、31、32，
依x的值分类，可设计三种方案：
①安排A种产品30件，B种产品20件；
②安排A种产品31件，B种产品19件；
③安排A种产品32件，B种产品18件．
（2）设安排生产A种产品x件，
那么利润为：y=700x+1200（50﹣x），整理得：y=﹣500x+60000，
∵k=﹣500＜0，∴y随x的增大而减小，x=30、31、32，
∴当x=30时，对应方案的利润最大，y=﹣500×30+60000=45000，最大利润为45000元．
∴当安排A种产品30件，B种产品20件，对应方案的利润最大，最大利润为45000元．
点睛: 本题考查了一次函数的应用,一元一次不等式组的应用及最大利润问题,得到两种原料的关系式和总利润的等量关系是解决本题的关键.
