Question

【题目】如图，在△ABC中，AB=AC，AD⊥BC于点D，BC=10cm，AD=8cm．点P从点B出发，在线段BC上以每秒3cm的速度向点C匀速运动，与此同时，垂直于AD的直线m从底边BC出发，以每秒2cm的速度沿DA方向匀速平移，分别交AB、AC、AD于E、F、H，当点P到达点C时，点P与直线m同时停止运动，设运动时间为t秒（t＞0）．
（1）当t=2时，连接DE、DF，求证：四边形AEDF为菱形；
（2）在整个运动过程中，问所形成的△PEF是否存在最大面积；如果存在请求出，如果不存在说明理由．
（3）是否存在某一时刻t，使△PEF为直角三角形？若存在，请求出此时刻t的值；若不存在，请说明理由．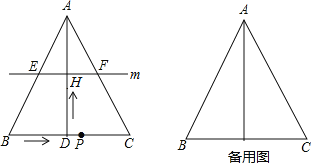

Answer 1

【答案】（1）证明见解析；（2）当t=2秒时，S△PEF存在最大值，最大值为10cm2；（3）当t＝秒，或t＝秒时，△PEF为直角三角形．

【解析】

（1）如答图1所示，利用菱形的定义证明；
（2）如答图2所示，首先求出△PEF的面积的表达式，然后利用二次函数的性质求解；
（3）如答图3所示，分三种情形，需要分类讨论，分别求解．

（1）证明：当t=2时，DH=AH=4，则H为AD的中点，如答图1所示．
又∵EF⊥AD，
∴EF为AD的垂直平分线，
∴AE=DE，AF=DF．
∵AB=AC，AD⊥BC于点D，
∴AD⊥BC，∠B=∠C．
∴EF∥BC，
∴∠AEF=∠B，∠AFE=∠C，
∴∠AEF=∠AFE，
∴AE=AF，
∴AE=AF=DE=DF，即四边形AEDF为菱形．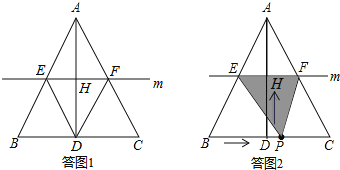

（2）解：如答图2所示，由（1）知EF∥BC，
∴△AEF∽△ABC，
∴ ，即 ，解得：EF=10-，
∴当t=2秒时，S△PEF存在最大值，最大值为10cm2．
（3）解：存在．理由如下：
①若点E为直角顶点，如答图3①所示，
此时PE∥AD，PE=DH=2t，BP=3t．
∵PE∥AD，
∴ ，
∴t=0（舍），故此种情形不存在；
②若点F为直角顶点，如答图3②所示，
此时PF∥AD，PF=DH=2t，BP=3t，CP=10-3t．
∵PF∥AD，∴，即 ，解得t=；

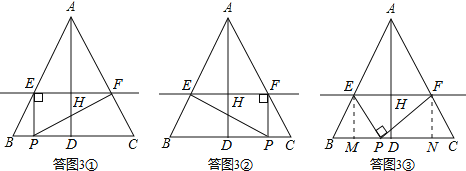
③若点P为直角顶点，如答图3③所示．
过点E作EM⊥BC于点M，过点F作FN⊥BC于点N，则EM=FN=DH=2t，EM∥FN∥AD．
∵EM∥AD，
∴，
即 ，
解得BM=t，
∴PM=BP-BM=3t-t=t．
在Rt△EMP中，由勾股定理得：PE2=EM2+PM2=（2t）2+（t）2=t2．
∵FN∥AD，
∴，
即 ，
解得CN=t，
∴PN=BC-BP-CN=10-3t-t=10- t．
在Rt△FNP中，由勾股定理得：PF2=FN2+PN2=（2t）2+（10-t）2=t2-85t+100．
在Rt△PEF中，由勾股定理得：EF2=PE2+PF2，
即：（10-t）2=（t2）+（t2-85t+100）
化简得：t2-35t=0，
解得：t=或t=0（舍去）
∴t=．
综上所述，当t=秒或t=秒时，△PEF为直角三角形．