题目内容
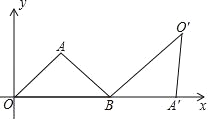
【题目】如图,点A的坐标为(3,![]() ),点B的坐标为(6,0),将△AOB绕点B按顺时针方向旋转一定的角度后得到△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为_____.
),点B的坐标为(6,0),将△AOB绕点B按顺时针方向旋转一定的角度后得到△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为_____.
【答案】(![]() ,
,![]() )
)
【解析】
作AC⊥OB、O′D⊥A′B,由点A、B坐标得出OC=3、AC=![]() 、BC=OC=3,从而知tan∠ABC=
、BC=OC=3,从而知tan∠ABC=![]() =
=![]() ,由旋转性质知BO′=BO=6,tan∠A′BO′=tan∠ABO=
,由旋转性质知BO′=BO=6,tan∠A′BO′=tan∠ABO=![]() =
=![]() ,设O′D=
,设O′D=![]() x、BD=3x,由勾股定理求得x的值,即可知BD、O′D的长即可.
x、BD=3x,由勾股定理求得x的值,即可知BD、O′D的长即可.
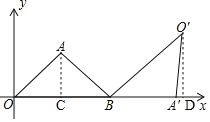
如图,过点A作AC⊥OB于C,过点O′作O′D⊥A′B于D,
∵A(3, ![]() ),
),
∴OC=3,AC=![]() ,
,
∵OB=6,
∴BC=OC=3,
则tan∠ABC=![]() =
=![]() ,
,
由旋转可知,BO′=BO=6,∠A′BO′=∠ABO,
∴![]() =
=![]() =
=![]() ,
,
设O′D=![]() x,BD=3x,
x,BD=3x,
由O′D2+BD2=O′B2可得(![]() x)2+(3x)2=62,
x)2+(3x)2=62,
解得:x=![]() 或x=
或x=![]() (舍),
(舍),
则BD=3x=![]() ,O′D=
,O′D=![]() x=
x=![]()
![]() ,
,
∴OD=OB+BD=6+![]() =
=![]() ,
,
∴点O′的坐标为(![]() ,
,![]() ).
).

练习册系列答案
相关题目