题目内容
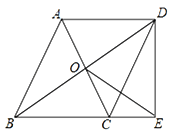
【题目】如图,□ABCD的对角线交于点O,点E在边BC的延长线上,且OE=OB,连接DE.
(1)求证:△BDE是直角三角形;
(2)如果OE⊥CD,试判断△BDE与△DCE是否相似,并说明理由.
【答案】(1)证明见解析;(2)相似,理由见解析.
【解析】试题分析:(1)由平行四边形ABCD 对角线互相平分、已知条件OE=OB以及等边对等角推知∠BED=∠OEB+∠OED=90°,则DE⊥BE,即△BDE是直角三角形;
(2)利用两角法证得△BDE与△DCE相似.
证明:(1)∵四边形ABCD是平行四边形,
∴OB=OD,
∵OE=OB, ∴OE=OD,
∴∠OBE=∠OEB,∠ODE=∠OED,
∵∠OBE+∠OEB+∠ODE+∠OED=180°,
∴∠BED=∠OEB+∠OED=90°,
∴DE⊥BE,即△BDE是直角三角形;
(2)△BDE与△DCE相似.
理由如下:
∵OE⊥CD,
∴∠CEO+∠DCE=∠CDE+∠DCE=90°,
∴∠CEO=∠CDE,
∵∠OBE=∠OEB,
∴∠DBE=∠CDE,
∵∠BED=∠DEC=90°,
∴△BDE∽△DCE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目