Question

【题目】如图,已知,,,，和交于点，则下列结论：①；②；③平分；④.其中正确的有____.

Answer 1

【答案】①②③④

【解析】

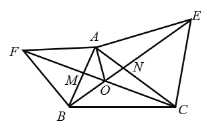
如图先证明△ABE≌△AFC，得到BE=CF，利用“8字型”证明∠CON=∠CAE=60°，从而得到∠BOC=180°-∠CON=120°；连接AO，过A分别作AP⊥CF与P，AM⊥BE于Q ，通过S△ABE=S△AFC，得到AP=AQ，利用角平分线的判定定理得AO平分∠EOF，在OE上截取OD=OA，连接AD，证明△AFO≌△BAD，再由此可以解决问题．

解：由题意可知AB=AF，AC=AE，∠FAB=∠EAC=60°，

∴∠FAB+∠BAC=∠EAC+∠BAC，

即∠FAC=∠BAE，

在△ABE与△AFC中， ，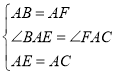

∴△ABE≌△AFC（SAS），

∴BE=FC，故①正确，∠AEB=∠ACF，

∵∠EAN+∠ANE+∠AEB=180°，∠CON+∠CNO+∠ACF=180°，∠ANE=∠CNO

∴∠CON=∠CAE=60°

∴∠BOC=180°-∠CON=120°，故②正确，

连接AO，过A分别作AP⊥CF与P，AM⊥BE于Q，如图，

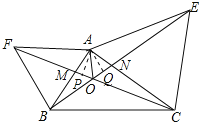
∵△ABE≌△AFC，

∴S△ABE=S△AFC，

∴CFAP=BEAQ，而CF=BE，

∴AP=AQ，

∴OA平分∠FOE，所以③正确，

在OE上截取OD=OA，连接AD

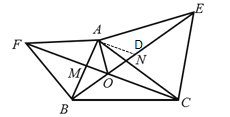
∵∠BOC=120°，AO平分∠FOE

∴∠AOD=60°

又∵OD=OA

∴△AOD为等边三角形

∴AD=AO；∠OAD=∠FAB=60°

∴∠OAD+∠BAO=∠FAB+∠BAO

∴∠FAO=∠BAD

又∵FA=AB

∴△AFO≌△BAD

∴OF=BD=BO+OD=BO+AO，④正确

故答案为：①②③④．