Question

【题目】如图1，在△ABC中，AB=AC，D，E分别在AB，AC上，AD=AE，将△ADE绕点A逆时针任意旋转.

（1）发现：如图2，连结BD，CE，若∠BAC=60°，D点恰在线段BE上，则∠BEC= °；

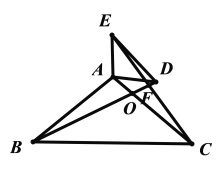
（2）探究：如图3，连结BD，CE，并交于点F，求证：∠BFC=∠BAC；

（3）拓展：如图4，若∠BAC=90°，AB=5，AD=2，连结CD，BE，请直接写出四边形BCDE的最大面积.

Answer 1

【答案】（1）60；（2）证明见解析；（3）.

【解析】

（1）首先可知是等边三角形，可得，根据邻补角的定义得，又易证，由三角形全等的性质得，最后根据即可得；

（2）由定理可证，由三角形全等的性质得，如图（见解析），设BD与AC的交点为点O，因，根据三角形内角和定理即得证；

（3）分析可知，要使四边形BCDE的最大面积，也就是要使和的面积最大，如图（见解析），过点E作，过点D作交CA延长线于点G，易证，由三角形全等的性质可得，从而可得和的面积相等，所以现在要求的是的最大面积，AC的长是定长，所以高GD要最大，可发现，当绕点A旋转到时，GD取得最大值AD，此时四边形BCDE由四个直角三角形组成，然后求其面积之和即可得出答案.

（1）由旋转的性质得：

是等边三角形

又

又

故答案为：60；

（2）如图，设BD与AC的交点为点O

由旋转的性质得：

又

，即

在中，由三角形内角和定理得：

在中，由三角形内角和定理得：

即；

（3）如图，过点E作，过点D作交CA延长线于点G

（旋转的性质）

又

由题意可知，要使四边形BCDE的最大面积，也就是要使和的面积最大

因此只要的面积最大即可

又因AC的长是定长，所以高GD要最大

当绕点A旋转到时，GD取得最大值AD

此时四边形BCDE由四个直角三角形组成

故四边形BCDE的最大面积为：

.