Question

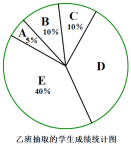
【题目】2019年是中华人民共和国成立70周年，某校将开展“爱我中华，了解历史”为主题的知识竞赛，八年级某老师为了解所任教的甲，乙两班学生相关知识的掌握情况，对两个班的学生进行了中国历史知识检测，满分为100分.现从两个班分别随机抽取了20名学生的检测成绩进行整理、描述和分析，下面给出了部分信息:(成绩得分用x表示，共分为五组，A组:0≤x＜80,B组:80≤x＜85,C组:85≤x＜90,D组:90≤x＜95,E组:95≤x≤100)

甲班20名学生的成绩为:

82，85，96，73，91，99，87，91，86，91

87, 94，89, 96，96，91，100，93，94, 99

乙班20名学生的成绩在D组中的数据是:91，92，92，92，92，93,94

甲，乙两班抽取的学生成绩数据统计表:

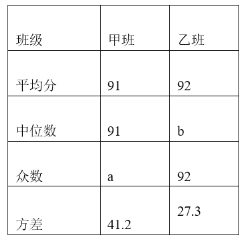
根据以上信息，解答下列问题:

(1)请直接写出上述统计表中a,b的值:a= ，b= ；

(2)若甲，乙两班总人数为120名，且都参加了此次知识检测，若规定成绩得分x≥95为优秀，请估计此次检测成绩优秀的学生人数是多少名?

Answer 1

【答案】（1）91，92.5；（2）42人

【解析】

（1）求出乙班D组的占比，进而求出E组的占比，求出a的值，根据中位数的意义，将乙班的抽查的20人成绩排序找出处在中间位置的两个数的平均数即可为中位数，从甲班成绩中找出出现次数最多的数即为众数；

（3）抽查甲班20人中优秀的有6，乙班20人中优秀有8人，因此两个班优秀占抽查人数，求出优秀人数即可．

解：（1）乙班D组所占的百分比为：=35%，

1-35%-10%-10%-5%=40%，

乙班ABC三组人数为20×（10%+10%+5%）=5人，
中位数是从小到大排列后处在第10、11位两个数的平均数，
由D组中的数据是：93，91，92，94，92，92，92可得处在第10、11位的两个数的平均数为（92+93）÷2=92.5，
因此b=92.5，
甲班的出现次数最多的是91，因此众数是91，即a=91．
故答案为：91，92.5．

（2）120×=42（人）

答：此次检测成绩优秀（x≥95）的学生人数是42人．