ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ‘ΡΕΝœ¬Ν–≤ΡΝœ≤ΔΆξ≥…»ΈΈώΘΚ
ΓΑΉνΕΧ¬ΖΨΕΈ ΧβΓ± « ΐ―ß÷–“ΜάύΨΏ”–Χτ’Ϋ–‘ΒΡΈ Χβ.Τδ ΒΘ§ ΐ―ß Ζ…œ“≤”–≤Μ…ΌœύΙΊΒΡΙ ¬Θ§»γœ¬Φ¥ΈΣΤδ÷–ΫœΈΣΨ≠ΒδΒΡ“Μ‘ρΘΚΙ≈œΘάΑ”–“ΜΈΜΨΟΗΚ ΔΟϊΒΡ―ß’ΏΘ§ΟϊΫ–ΚΘ¬Ή.ΥϊΨΪΆ® ΐ―ßΓΔΈοάμΘ§¥œΜέΙΐ»Υ.”–“ΜΧλΘ§“ΜΈΜΫΪΨϋœρΥϊ«κΫΧ“ΜΗωΈ ΧβΘΚ»γΆΦ1Θ§ΫΪΨϋ¥”ΦΉΒΊΤο¬μ≥ωΖΔΘ§“ΣΒΫΚ”±Ώ»Ο¬μ“ϊΥ°Θ§»ΜΚσ‘ΌΜΊΒΫ““ΒΊΒΡ¬μ≈οΘ§ΈΣ Ι¬μΉΏΒΡ¬Ζ≥ΧΉνΕΧΘ§”ΠΗϻϬ쑾 ≤ϥºΖΫ“ϊΥ°ΘΩ
ΚΘ¬Ή»œΈΣ“‘Κ”±ΏΈΣΨΒΟφΘ§Μ≠≥ωΦΉΒΊΒΡΨΒœώΒψΘ®¥Ι÷±Κ”±ΏΒΡΒ»ΨύάκΒψΘ©Θ§»ΜΚσΝ§Ϋ”““ΒΊΚΆΦΉΒΊΒΡΨΒœώΒψΘ§ΜαΗζΚ”±ΏœύΫΜ“ΜΒψΘ§’βΗωΒψΨΆ «¬μ“ϊΥ°ΒΡΒΊΖΫΘ§¬μΉΏΒΡ¬Ζ≥ΧΉνΕΧΘ®ΝΫΒψ÷°Φδ÷±œΏΨύάκΉνΕΧΘ©.

»ΈΈώΘΚ
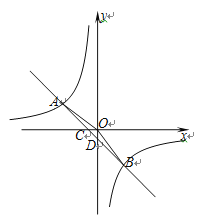
Θ®1Θ©«κΡψΑοΚΘ¬Ή‘ΎΆΦ1ΒΡΈΜ÷ΟΆξ≥…ΉςΆΦΘ§≤Δ±ξ≥ω¬μ“ϊΥ°ΒΡΒΊΒψ![]() Θ®Μ≠≥ω≤ίΆΦΦ¥Ω…Θ©ΘΜ
Θ®Μ≠≥ω≤ίΆΦΦ¥Ω…Θ©ΘΜ
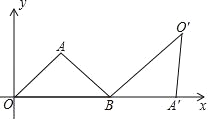
Θ®2Θ©»γΆΦ2Θ§![]() ΒΡ»ΐΗωΕΞΒψΒΡΉχ±ξΖ÷±πΈΣ
ΒΡ»ΐΗωΕΞΒψΒΡΉχ±ξΖ÷±πΈΣ![]() Θ§
Θ§![]() Θ§
Θ§![]() .«κΡψ‘Ύ
.«κΡψ‘Ύ![]() ÷α…œ’““ΜΒψ
÷α…œ’““ΜΒψ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() Ήν–ΓΘ§≤Δ÷±Ϋ”–¥≥ωΒψ
Ήν–ΓΘ§≤Δ÷±Ϋ”–¥≥ωΒψ![]() ΒΡΉχ±ξΘ®±ΘΝτΉςΆΦΚέΦΘΘ©ΘΜ
ΒΡΉχ±ξΘ®±ΘΝτΉςΆΦΚέΦΘΘ©ΘΜ

”Π”ΟΘΚ
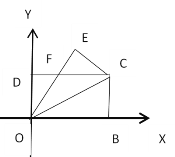
Θ®3Θ©»γΆΦ3Θ§‘≤÷υ–Έ»ίΤςΗΏΈΣ![]() Θ§ΒΉΟφ÷ή≥ΛΈΣ
Θ§ΒΉΟφ÷ή≥ΛΈΣ![]() Θ§‘Ύ±≠ΡΎ±Ύάκ±≠ΒΉ
Θ§‘Ύ±≠ΡΎ±Ύάκ±≠ΒΉ![]() ΒΡΒψ
ΒΡΒψ![]() ¥Π”–“ΜΒΈΖδΟέΘ§¥Υ ±“Μ÷Μ¬λ“œ’ΐΚΟ‘Ύ±≠Άβ±ΎΘ§άκ±≠…œ―Ί
¥Π”–“ΜΒΈΖδΟέΘ§¥Υ ±“Μ÷Μ¬λ“œ’ΐΚΟ‘Ύ±≠Άβ±ΎΘ§άκ±≠…œ―Ί![]() ¥ΠΒΡΒψ
¥ΠΒΡΒψ![]() ¥ΠΘ§Βψ
¥ΠΘ§Βψ![]() ”κ
”κ![]() ΒΡΥ°ΤΫΨύάκΒ»”ΎΒΉΟφ÷±ΨΕΘ§«σ¬λ“œ¥”Άβ±Ύ
ΒΡΥ°ΤΫΨύάκΒ»”ΎΒΉΟφ÷±ΨΕΘ§«σ¬λ“œ¥”Άβ±Ύ![]() ¥ΠΒΫ¥οΡΎ±Ύ
¥ΠΒΫ¥οΡΎ±Ύ![]() ¥ΠΒΡΉνΕΧΨύάκ.
¥ΠΒΡΉνΕΧΨύάκ.

ΓΨ¥πΑΗΓΩΘ®1Θ©œξΦϊΫβΈωΘΜΘ®2Θ©ΆΦœξΦϊΫβΈωΘ§Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() ΘΜΘ®3Θ©¬λ“œ¥”Άβ±Ύ
ΘΜΘ®3Θ©¬λ“œ¥”Άβ±Ύ![]() ¥ΠΒΫ¥οΡΎ±Ύ
¥ΠΒΫ¥οΡΎ±Ύ![]() ¥ΠΒΡΉνΕΧΨύάκΈΣ
¥ΠΒΡΉνΕΧΨύάκΈΣ![]() .
.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨί‘ΎΚ”±Ώ…œΒΡΆ§≤ύ”–ΝΫΗωΒψAΓΔBΘ§‘Ύ÷±œΏL…œ”–ΒΫAΓΔBΒΡΨύάκ÷°ΚΆΉνΕΧΒΡΒψ¥φ‘ΎΘ§Ω…“‘Ά®Ιΐ÷αΕ‘≥Τά¥»ΖΕ®Θ§Φ¥Ής≥ωΤδ÷–“ΜΒψΙΊ”Ύ÷±œΏlΒΡΕ‘≥ΤΒψΘ§Ε‘≥ΤΒψ”κΝμ“ΜΒψΒΡΝ§œΏ”κΚ”±ΏœΏΒΡΫΜΒψΨΆ «Υυ“Σ’“ΒΡΒψΘ°
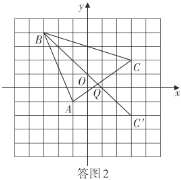
Θ®2Θ©’“≥ωCΒΡΕ‘≥ΤΒψCΓδΘ§Ν§Ϋ”BCΓδΘ§”κx÷αΫΜΒψΦ¥ΈΣQΘΜ
Θ®3Θ©ΫΪ±≠Ή”≤ύΟφ’ΙΩΣΘ§Ϋ®ΝΔAΙΊ”ΎEFΒΡΕ‘≥ΤΒψAΓδΘ§ΗυΨίΝΫΒψ÷°ΦδœΏΕΈΉνΕΧΩ…÷ΣAΓδBΒΡ≥ΛΕ»Φ¥ΈΣΥυ«σΘ°
ΫβΘΚΘ®1Θ©»γ¥πΆΦ1Φ¥ΈΣΥυΉςΆΦ–Έ.
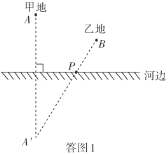
Θ®2Θ©»γ¥πΆΦ2Θ§Βψ![]() Φ¥ΈΣΥυ«σ.
Φ¥ΈΣΥυ«σ.
Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]()
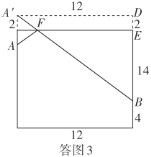
Θ®3Θ©»γ¥πΆΦ3 «±≠Ή”ΒΡ≤ύΟφΒΡ≤ΩΖ÷’ΙΩΣΆΦΘ§
…ηΒψ![]() ΈΣ±≠Ή”≤ύΟφ’ΙΩΣΆΦ…œ±Ώ―ΊΒΡ÷–ΒψΘ§ΉςΒψ
ΈΣ±≠Ή”≤ύΟφ’ΙΩΣΆΦ…œ±Ώ―ΊΒΡ÷–ΒψΘ§ΉςΒψ![]() ΙΊ”Ύ…œ±Ώ―ΊΒΡΕ‘≥ΤΒψ
ΙΊ”Ύ…œ±Ώ―ΊΒΡΕ‘≥ΤΒψ![]() Θ§
Θ§
Ν§Ϋ”![]() Θ§‘ρ
Θ§‘ρ![]() Φ¥ΈΣΉνΕΧΨύάκΘ§
Φ¥ΈΣΉνΕΧΨύάκΘ§
…η![]() ”κ’ΙΩΣΆΦΒΡ…œ±Ώ‘ΒΫΜ”ΎΒψ
”κ’ΙΩΣΆΦΒΡ…œ±Ώ‘ΒΫΜ”ΎΒψ![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() Ής
Ής![]() Θ§«“”κ
Θ§«“”κ![]() ΒΡ―”≥ΛœΏΫΜ”ΎΒψ
ΒΡ―”≥ΛœΏΫΜ”ΎΒψ![]() Θ§
Θ§
‘ρ![]() Θ§
Θ§
![]() .
.
‘Ύ![]() ÷–Θ§
÷–Θ§
![]() .
.
Γύ¬λ“œ¥”Άβ±Ύ![]() ¥ΠΒΫ¥οΡΎ±Ύ
¥ΠΒΫ¥οΡΎ±Ύ![]() ¥ΠΒΡΉνΕΧΨύάκΈΣ
¥ΠΒΡΉνΕΧΨύάκΈΣ![]() .
.