题目内容
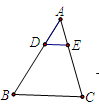
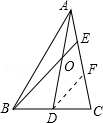
如图,在△ABC中,D为BC边的中点,E为AC边上的任意一点,BE交AD与点O,某学生在研究这一问题时,发现了如下事实,
①当 ;
;
②当 ;
;
③ ;
;
如图4中,当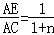 时,请你猜想
时,请你猜想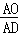 的一般结论,并证明你的结论(其中n为正整数).
的一般结论,并证明你的结论(其中n为正整数).
①当
 ;
;②当
 ;
;③
 ;
;如图4中,当
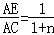 时,请你猜想
时,请你猜想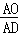 的一般结论,并证明你的结论(其中n为正整数).
的一般结论,并证明你的结论(其中n为正整数).
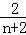 理由见解析
理由见解析试题分析: 过D作DF∥BE,即求AO:AD=AE:AF,因为
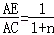 ,可以根据平行线分线段成比例,及线段相互间的关系即可得出AE:AF=2:(n+2),即
,可以根据平行线分线段成比例,及线段相互间的关系即可得出AE:AF=2:(n+2),即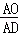 =
=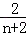 .
.解:猜想
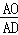 =
=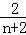 .
.证明:过D作DF∥BE,
∴AO:AD=AE:AF.
∵D为BC边的中点,
∴CF=EF=
 EC.
EC.∵
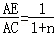 ,
,∴AE:(AE+2EF)=1:(1+n).
∴AE:EF=2:n.
∴AE:AF=2:(n+2),即
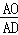 =
=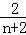 .
.
点评:本题考查平行线分线段定理及其应用,有一定难度,注意D为BC边的中点的运用.

练习册系列答案
相关题目
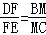 .
.
 的值是 _________ .
的值是 _________ .

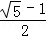 AB;③PB=
AB;③PB=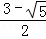 AB;④
AB;④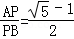 ;⑤
;⑤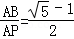 .其中正确的是 (填“序号”)
.其中正确的是 (填“序号”)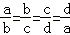 ,求
,求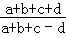 的值.
的值.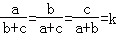 ,则直线y=kx+2k一定经过()
,则直线y=kx+2k一定经过()