题目内容
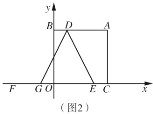
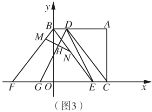
【题目】小明坐于堤边垂钓，如图①，河堤AC的坡角为30°，AC长
米，钓竿AO的倾斜角是60°，其长为3米，若AO与钓鱼线OB的夹角为60°，求浮漂B与河堤下端C之间的距离(如图②)．
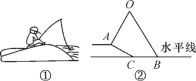
【答案】1．5米．
【解析】
试题延长OA交BC于点D．先由倾斜角定义及三角形内角和定理求出
在Rt△ACD中,
米，CD=2AD=3米，再证明△BOD是等边三角形，得到
米，然后根据BC=BDCD即可求出浮漂B与河堤下端C之间的距离．
试题解析：延长OA交BC于点D.
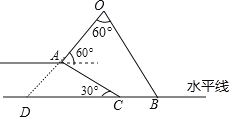
∵AO的倾斜角是
，
∴
∵
在Rt△ACD中,
(米)，
∴CD=2AD=3米，
又
∴△BOD是等边三角形，
∴(米)，
∴BC=BDCD=4.53=1.5(米).
答：浮漂B与河堤下端C之间的距离为1.5米.
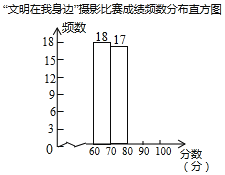
阅读快车系列答案【题目】某校举行了“文明在我身边”摄影比赛，已知每幅参赛作品成绩记为x分(60≤x≤100)．校方从600幅参赛作品中随机抽取了部分步赛作品，统计了它们的成绩，并绘制了如下不完整的统计图表．
“文明在我身边”摄影比赛成绩统计表
分数段 | 频数 | 频率 |
60≤x<70 | 18 | 0.36 |
70≤x<80 | 17 | c |
80≤x<90 | a | 0.24 |
90≤x≤100 | b | 0.06 |
合计 | 1 |
根据以上信息解答下列问题：
（1）统计表中a= ，b= ，c= ．
（2）补全数分布直方图；
（3）若80分以上的作品将被组织展评，试估计全校被展评作品数量是多少？
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共50个，小颖做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是试验中的一组统计数据：
摸到球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的概率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
（1）请估计当
很大时，摸到白球的频率将会接近______；（精确到0.1）；
（2）假如随机摸一次，摸到白球的概率P（白球）＝______；
（3）试估算盒子里白色的球有多少个？
