Question

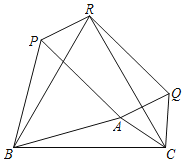
【题目】以△ABC的三边为边在BC的同一侧作等边△ABP，等边△ACQ，等边△BCR．

（1）四边形QRPA是平行四边形吗？若是，请证明；若不是，请说明理由．

（2）当△ABC满足什么条件时，四边形QRPA是矩形？请说明理由．

Answer 1

【答案】（1）四边形QRPA是平行四边形，理由详见解析；（2）当∠BAC＝150°时，四边形QRPA是矩形，理由详见解析

【解析】

（1）由“SAS”可证△BRP≌△BCA，△CAB≌△CQR，可得PR＝AC，AB＝RQ，可得RP＝AQ，AP＝RQ，可得结论；

（2）当∠BAC＝150时，由周角的性质可求∠PAQ＝90，可证平行四边形QRPA是矩形．

证明：（1）四边形QRPA是平行四边形

理由如下：∵等边△ABP，等边△ACQ，等边△BCR，

∴AB＝PB，BC＝BR＝CR，AC＝CQ，∠PBA＝∠RBC＝∠BCR＝∠ACQ＝60，

∴∠PBR＝∠ABC，∠ACB＝∠QCR，

∴△BRP≌△BCA（SAS），

∴PR＝AC，

∵BC＝RC，∠BCA＝∠RCQ，AC＝CQ，

∴△CAB≌△CQR（SAS）

∴AB＝RQ，

∴RP＝AQ，AP＝RQ，

∴四边形QRPA是平行四边形；

（2）当∠BAC＝150时，四边形QRPA是矩形，

∵∠PAQ+∠BAP+∠CAQ+∠BAC＝360，

∴∠PAQ＝360﹣60﹣60﹣150＝90，

∴平行四边形QRPA是矩形．