Question

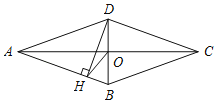
【题目】如图，四边形ABCD是菱形，对角线AC，BD相交于点O，DH⊥AB于点H，连接OH，若∠DHO＝20°，则∠ADC的度数是（　　）

A. 120°B. 130°C. 140°D. 150°

Answer 1

【答案】C

【解析】

由四边形ABCD是菱形，可得OB＝OD，AC⊥BD，又由DH⊥AB，∠DHO＝20°，可求得∠OHB的度数，然后由直角三角形斜边上的中线等于斜边的一半，证得△OBH是等腰三角形，继而求得∠ABD的度数，然后求得∠ADC的度数．

∵四边形ABCD是菱形，

∴OB＝OD，AC⊥BD，∠ADC＝∠ABC，

∵DH⊥AB，

∴OH＝OB＝BD，

∵∠DHO＝20°，

∴∠OHB＝90°﹣∠DHO＝70°，

∴∠ABD＝∠OHB＝70°，

∴∠ADC＝∠ABC＝2∠ABD＝140°，

故选C．