题目内容
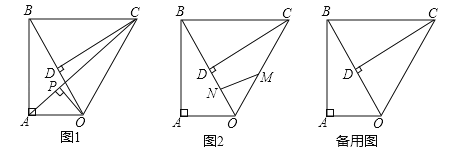
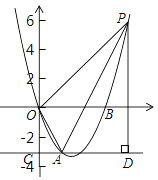
【题目】如图,已知抛物线![]() 过点A(
过点A(![]() ,-3) 和B(3
,-3) 和B(3![]() ,0),过点A作直线AC//x轴,交y轴与点C.
,0),过点A作直线AC//x轴,交y轴与点C.
(1)求抛物线的解析式;
(2)在抛物线上取一点P,过点P作直线AC的垂线,垂足为D,连接OA,使得以A,D,P为顶点的三角形与△AOC相似,求出对应点P的坐标;
(3)抛物线上是否存在点Q,使得![]() ?若存在,求出点Q的坐标;若不存在,请说明理由.
?若存在,求出点Q的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)P点坐标为(4
;(2)P点坐标为(4![]() ,6)或(
,6)或(![]() ,-
,- ![]() );(3)Q点坐标(3
);(3)Q点坐标(3![]() ,0)或(-2
,0)或(-2![]() ,15)
,15)
【解析】
(1)把A与B坐标代入抛物线解析式求出a与b的值,即可确定出解析式;
(2)设P坐标为![]() ,表示出AD与PD,由相似分两种情况得比例求出x的值,即可确定出P坐标;
,表示出AD与PD,由相似分两种情况得比例求出x的值,即可确定出P坐标;
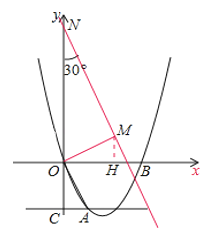
(3)存在,求出已知三角形AOC边OA上的高h,过O作OM⊥OA,截取OM=h,与y轴交于点N,分别确定出M与N坐标,利用待定系数法求出直线MN解析式,与抛物线解析式联立求出Q坐标即可.
(1)把![]() ,
,![]() 和点
和点![]() ,
,![]() 代入抛物线得:
代入抛物线得:![]() ,
,
解得:![]() ,
,![]() ,
,
则抛物线解析式为![]() ;
;
(2)当![]() 在直线
在直线![]() 上方时,
上方时,
设![]() 坐标为
坐标为![]() ,则有
,则有![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,
,
整理得:![]() ,即
,即![]() ,
,
解得:![]() ,即
,即![]() 或
或![]() (舍去),
(舍去),
此时![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ,
,
整理得:![]() ,即
,即![]() ,
,
解得:![]() ,即
,即![]() 或
或![]() (舍去),
(舍去),
此时![]() ,
,![]() ;
;
当点![]() 时,也满足
时,也满足![]() ;
;
当![]() 在直线
在直线![]() 下方时,同理可得:
下方时,同理可得:![]() 的坐标为
的坐标为![]() ,
,![]() ,
,
综上,![]() 的坐标为
的坐标为![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ;
;
(3)在![]() 中,
中,![]() ,
,![]() ,
,
根据勾股定理得:![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() 边
边![]() 上的高为
上的高为![]() ,
,
过![]() 作
作![]() ,截取
,截取![]() ,过
,过![]() 作
作![]() ,交
,交![]() 轴于点
轴于点![]() ,如图所示:
,如图所示:
在![]() 中,
中,![]() ,即
,即![]() ,
,
过![]() 作
作![]() 轴,
轴,
在![]() 中,
中,![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
设直线![]() 解析式为
解析式为![]() ,
,
把![]() 坐标代入得:
坐标代入得:![]() ,即
,即![]() ,即
,即![]() ,
,
联立得: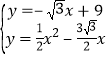 ,
,
解得:![]() 或
或![]() ,即
,即![]() ,
,![]() 或
或![]() ,
,![]() ,
,
则抛物线上存在点![]() ,使得
,使得![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]() ,
,![]() 或
或![]() ,
,![]() .
.

【题目】(9分)九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为![]() 元.
元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 元;②月销量是 件;(直接写出结果)
(2)设销售该运动服的月利润为![]() 元,那么售价为多少时,当月的利润最大,最大利润是多少?
元,那么售价为多少时,当月的利润最大,最大利润是多少?