题目内容
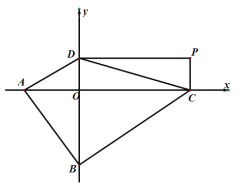
【题目】如图,点A是反比例函数![]() 图象第一象限上一点,过点A作
图象第一象限上一点,过点A作![]() 轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点
轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点![]() 记
记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,连接BC,则
,连接BC,则![]() 是______三角形,若
是______三角形,若![]() 的值最大为1,则k的值为______.
的值最大为1,则k的值为______.
【答案】 等腰直角; ![]()
【解析】分析:
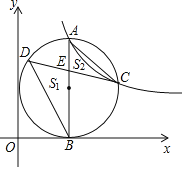
(1)如下图,连接O′C,过点C作CH⊥x轴于点H,由![]() O′和两坐标轴相切可知
O′和两坐标轴相切可知![]() O′和反比例函数
O′和反比例函数![]() 的图象都关于直线y=x对称,若设点A的坐标为(m,2m),则点C的坐标为(2m,m),结合题意易证四边形BHCO′是正方形,从而可得∠ABC=45°,由AB为
的图象都关于直线y=x对称,若设点A的坐标为(m,2m),则点C的坐标为(2m,m),结合题意易证四边形BHCO′是正方形,从而可得∠ABC=45°,由AB为![]() O′直径可得∠ACB=90°,由此可得△ABC是等腰直角三角形;
O′直径可得∠ACB=90°,由此可得△ABC是等腰直角三角形;
(2)由下图,连接DO′,并延长交BC于点F,由已知易得S1-S2=S△BCD-S△ABC, S△ABC是定值,BC是定值,从而可得当DF最长,即当DF⊥BC时,S1-S2的值最大,用含m的代数式表达出S△BCD和S△ABC的面积,结合S1-S2的最大值为1列出方程,解方程求得m的值即可得到点A的坐标,从而可得k的值.
详解:
(1)如下图,连接O′C,过点C作CH⊥x轴于点H,由![]() O′和两坐标轴相切可知
O′和两坐标轴相切可知![]() O′和反比例函数
O′和反比例函数![]() 的图象都关于直线y=x对称,
的图象都关于直线y=x对称,
∴若设点A的坐标为(m,2m),则点C的坐标为(2m,m),
∴BO′=CH=m,BO′∥CH,
∴四边形BHCO′是平行四边形,
∵BH=CH,∠BHC=90°,
∴四边形BHCO′是正方形.
∴∠ABC=45°,
∵AB为![]() O′直径,
O′直径,
∴∠ACB=90°,
∴△ACB是等腰直角三角形;
(2)由下图,连接DO′,并延长交BC于点F,
∵由图可得S1-S2=S△BCD-S△ABC, S△ABC是定值,BC是定值,
∴当DF最长,即当DF⊥BC时,S1-S2的值最大,
∵△ABC中,∠ACB=90°,∠ABC=45°,AB=2m,且DF⊥BC,
∴BC=AC=![]() ,DF=DO′+O′F=
,DF=DO′+O′F=![]() ,
,
又∵S1-S2=S△BCD-S△ABC=1,
∴![]() ,
,
化简得:![]() ,
,
∵点A(m,2m)在反比例函数函数![]() 的图象上,
的图象上,
∴k=2m2=![]() .
.
故答案为:(1)等腰直角;(2)![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案