题目内容
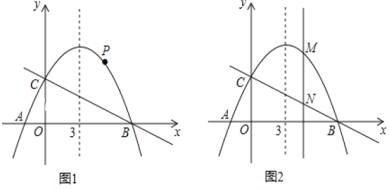
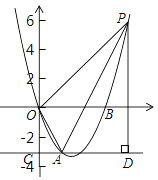
【题目】如图，已知抛物线y=ax2-4x+c(a≠0)与反比例函数y=
的图象相交于B点，且B点的横坐标为3，抛物线与y轴交于点C(0,6)，A是抛物线y=ax2-4x+c的顶点，P点是x轴上一动点，当PA+PB最小时，P点的坐标为_______．
【答案】(
，0)
【解析】
根据题意作出合适的辅助线，然后求出点B的坐标，从而可以求得二次函数解析式，然后求出点A的坐标，进而求得A＇的坐标，从而可以求得直线A＇B的函数解析式，进而求得与x轴的交点，从而可以解答本题
解：作点A关于x轴的对称点A＇，连接A＇B，则A＇B与x轴的交点即为所求，
∵抛物线y=ax2-4x+c(a
0)与反比例函数y=
的图象相交于点B，且B点的横坐标为3，抛物线与y轴交于点C（0,6），
∴点B（3,3），
∴
解得，
∴y=x2-4x+6=（x-2）2+2
∴点A的坐标为（2,2），
∴点A＇的坐标为（2，-2），
设过点A＇（2，-2）和点B（3,3）的直线解析式为y=mx+n
∴
∴直线A＇B的函数解析式为y=5x-12,
令y=0,则0=5x-12得x=,
故答案为：（
）
练习册系列答案
相关题目
