题目内容
【题目】已知二次函数y=ax2+bx+c的图象经过点A（-1，0），B（1，4），C（0，3）．
（1）求出此二次函数的表达式，并把它化成
的形式；
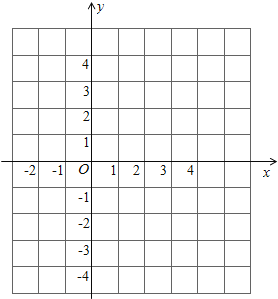
（2）请在坐标系内画出这个函数的图象，并根据图象写出函数值y为负数时，自变量x的取值范围．
【答案】（1）
；（2）见解析.
【解析】
1）设函数解析式为y=ax2+bx+c，将A（-1，0），B（1，4），C（0，3）分别代入解析式，得到三元一次方程组，求解即可得二次函数的一般式；再用配方法得到顶点式；
（2）求出顶点坐标、图象与x轴、y轴的交点，连接各点，即可得到函数的图象．
（1）（1）将A（-1，0），B（1，4），C（0，3）分别代入解析式y=ax2+bx+c，得，
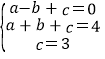，解得，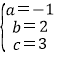
，
则函数解析式为y=-x2+2x+3．
即y=-（x2-2x-3）=-（x2-2x+1-4）=-（x-1）2+4；
（2）根据y=-（x-1）2+4可知，
其顶点坐标为（1，4），
又当y=0时，-x2+2x+3=0，
x1=-1，x2=3．
则图象与x轴的交点坐标为（-1，0），（3，0）．
当x=0时，y=3．
故函数图象与y轴的交点为（0，3）．故可得函数图象为：
练习册系列答案
相关题目
