题目内容
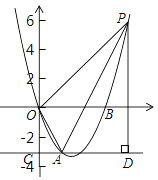
【题目】已知![]() ,
,![]() ,
,![]() ,斜边
,斜边![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,如图1,连接
,如图1,连接![]() .
.
(1)填空:![]()
![]() ;
;
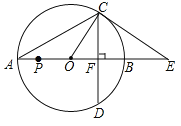
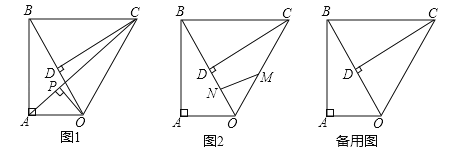
(2)如图1,连接![]() ,作
,作![]() ,垂足为
,垂足为![]() ,求
,求![]() 的长度;
的长度;
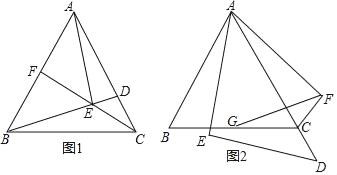
(3)如图2,点![]() ,
,![]() 同时从点
同时从点![]() 出发,在
出发,在![]() 边上运动,
边上运动,![]() 沿
沿![]() 路径匀速运动,
路径匀速运动,![]() 沿
沿![]() 路径匀速运动,当两点相遇时运动停止,已知点
路径匀速运动,当两点相遇时运动停止,已知点![]() 的运动速度为1.5单位
的运动速度为1.5单位![]() 秒,点
秒,点![]() 的运动速度为1单位
的运动速度为1单位![]() 秒,设运动时间为
秒,设运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,求当
,求当![]() 为何值时
为何值时![]() 取得最大值?最大值为多少?
取得最大值?最大值为多少?
【答案】(1)60;(2)![]() ;(3)x
;(3)x![]() 时,y有最大值,最大值
时,y有最大值,最大值![]() .
.
【解析】
(1)只要证明△OBC是等边三角形即可;
(2)求出△AOC的面积,利用三角形的面积公式计算即可;
(3)分三种情形讨论求解即可解决问题:①当0<x![]() 时,M在OC上运动,N在OB上运动,此时过点N作NE⊥OC且交OC于点E.②当
时,M在OC上运动,N在OB上运动,此时过点N作NE⊥OC且交OC于点E.②当![]() x≤4时,M在BC上运动,N在OB上运动.③当4<x≤4.8时,M、N都在BC上运动,作OG⊥BC于G.
x≤4时,M在BC上运动,N在OB上运动.③当4<x≤4.8时,M、N都在BC上运动,作OG⊥BC于G.
(1)由旋转性质可知:OB=OC,∠BOC=60°,
∴△OBC是等边三角形,
∴∠OBC=60°.
故答案为:60.
(2)如图1中。
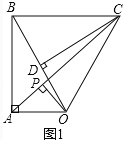
∵OB=4,∠ABO=30°,
∴OA![]() OB=2,AB
OB=2,AB![]() OA=2
OA=2![]() ,
,
∴S△AOC![]() OAAB
OAAB![]() 2×2
2×2![]() .
.
∵△BOC是等边三角形,
∴∠OBC=60°,∠ABC=∠ABO+∠OBC=90°,
∴AC![]() ,
,
∴OP![]() .
.
(3)①当0<x![]() 时,M在OC上运动,N在OB上运动,此时过点N作NE⊥OC且交OC于点E.
时,M在OC上运动,N在OB上运动,此时过点N作NE⊥OC且交OC于点E.
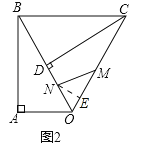
则NE=ONsin60°![]() x,
x,
∴S△OMN![]() OMNE
OMNE![]() 1.5x
1.5x![]() x,
x,
∴y![]() x2,
x2,
∴x![]() 时,y有最大值,最大值
时,y有最大值,最大值![]() .
.
②当![]() x≤4时,M在BC上运动,N在OB上运动.
x≤4时,M在BC上运动,N在OB上运动.
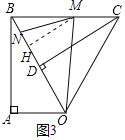
作MH⊥OB于H.
则BM=8﹣1.5x,MH=BMsin60°![]() (8﹣1.5x),
(8﹣1.5x),
∴y![]() ON×MH
ON×MH![]() x2+2
x2+2![]() x.
x.
当x![]() 时,y取最大值,y
时,y取最大值,y![]() ,
,
③当4<x≤4.8时,M、N都在BC上运动,
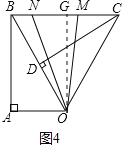
作OG⊥BC于G.MN=12﹣2.5x,OG=AB=2![]() ,
,
∴y![]() MNOG=12
MNOG=12![]() x,
x,
当x=4时,y有最大值,最大值=2![]() .
.
综上所述:y有最大值,最大值为![]() .
.