Question

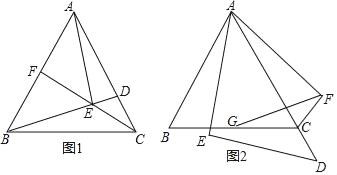
【题目】如图，已知，梯形中，，，∥，，，点在边上，以点为圆心为半径作弧交边于点，射线与射线交于点.

（1）若，求的长；

（2）联结，若，求的长；

（3）线段上是否存在点，使得△与△相似，若相似，求的值，若不相似，请说明理由

Answer 1

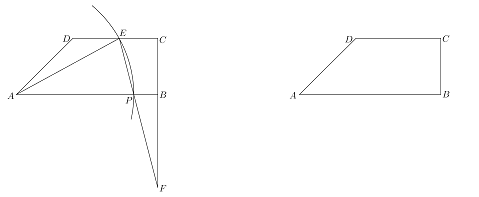
【答案】（1）1；（2）；（3）存在，FG＝3－1

【解析】

（1）如图所示，作DO⊥AB，垂足为O，先求出DO的长，然后根据勾股定理可求出DE的长；（2）如图作EQ⊥AB，垂足为Q，先根据HL证明Rt△EQP≌Rt△CBP，得到PB＝PQ，设PB＝x，则PQ＝x，AP＝5－x，根据勾股定理列一元二次方程，求解即可；（3）先根据三角形相似求出∠EAB的大小，然后根据特殊角的三角函数求出AD、DE、GD的长，再根据相似三角形对应边成比例即可求出FG的长.

（1）如图所示，作DO⊥AB，垂足为O.

∵DC＝3，AB＝5，

∴AO＝2，

又∵∠A＝45°，∴DO＝2，

依题意易知，AE＝AP＝，

根据勾股定理，AE2＝（AO＋DE）2＋DO2，即（2＋DE）2＋4＝13，

解得DE＝﹣5（舍去）或1，

∴DE＝1，

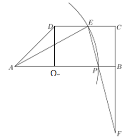
（2）如图作EQ⊥AB，垂足为Q.

∵CP＝EP，EQ＝CB，∴Rt△EQP≌Rt△CBP，

∴PB＝PQ，

设PB＝x，则PQ＝x，AP＝5－x，

由（1）知CB＝EQ＝2，

又∵AE＝AP＝5－x，

根据勾股定理有AE2＝AQ2＋EQ2，即（5－x）2＝（5－2x）2＋4，

解得x＝或，

∴AP＝（＜AD，舍去）或，

综上，AP＝.

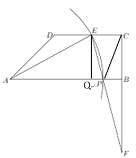
（3）∵∠F＋∠FPB＝90°，∠EAB＋2∠APE＝180°，∠APE＝∠FPB，

∴∠EAB＝2∠F，

若存在三角形相似，则∠DAE＝∠F，

又∵∠A＝45°，∴∠EAB＝30°，

如图所示，延长CD，作AH⊥CD，垂足为H，

AH＝DH＝2，EH＝2，

∴DE＝2－2，CE＝5－2，

∵∠EGF＝∠ADE＝135°，

∴∠EGC＝45°，

∴EG＝CE＝5，

∵△ADE∽△FGE，

∴，即，

∴FG＝3－1.