ƒøƒ⁄»ð
°æƒø°ø»Ù“ª∏ˆ»˝Ω«–Œ“ªÃı±þµƒ∆Ω∑Ωµ»”⁄¡Ì¡ΩÃı±þµƒ≥Àª˝£¨Œ“√«∞—’‚∏ˆ»˝Ω«–ŒΩ–◊ˆ±»¿˝»˝Ω«–Œ£Æ

£®1£©“—÷™°˜ABC «±»¿˝»˝Ω«–Œ£¨AB£Ω2£¨BC£Ω3£¨«Î÷±Ω”–¥≥ˆÀ˘”–¬˙◊„Ãıº˛µƒACµƒ≥§£ª
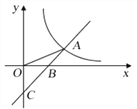
£®2£©»ÁÕº1£¨‘⁄Àƒ±þ–ŒABCD÷–£¨AD°ŒBC£¨∂‘Ω«œþBD∆Ω∑÷°œABC£¨°œBAC£Ω°œADC£Æ
¢Ÿ«Û÷§£∫°˜ABC°◊°˜DCA£ª¢⁄«Û÷§£∫°˜ABC «±»¿˝»˝Ω«–Œ£ª
£®3£©»ÁÕº2£¨‘⁄£®2£©µƒÃıº˛œ¬£¨µ±°œADC£Ω90°„ ±£¨«Û≥ˆ![]() µƒ÷µ£Æ
µƒ÷µ£Æ
°æ¥∞∏°ø£®1£©AC£Ω![]() ªÚ
ªÚ![]() ªÚ
ªÚ![]() £ª£®2£©¢Ÿº˚Ω‚Œˆ£ª¢⁄º˚Ω‚Œˆ£ª£®3£©
£ª£®2£©¢Ÿº˚Ω‚Œˆ£ª¢⁄º˚Ω‚Œˆ£ª£®3£©![]() £Ω
£Ω![]() £Æ
£Æ
°æΩ‚Œˆ°ø
£®1£©∏˘æ𱻿˝»˝Ω«–Œµƒ∂®“Â∑÷AB2£ΩBCAC°¢BC2£ΩABAC°¢AC2£ΩABBC»˝÷÷«Èøˆ∑÷±¥˙»Îº∆À„ø…µ√£ª
£®2£©¢Ÿœ»≈–∂œ≥ˆ°œACB£Ω°œCAD£¨µ√≥ˆ°˜ABC°◊°˜DCA£ª
¢⁄”…°˜ABC°◊°˜DCAµ√≥ˆCA2£ΩBCAD£¨‘Ÿ”…°œADB£Ω°œCBD£Ω°œABD÷™AB£ΩADº¥ø…µ√£ª
£®3£©◊˜AH°ÕBD£¨”…AB£ΩAD÷™£¨BH£Ω![]() BD£¨‘Ÿ÷§°˜ABH°◊°˜DBCµ√ABBC£ΩBHDB£¨º¥ABBC£Ω
BD£¨‘Ÿ÷§°˜ABH°◊°˜DBCµ√ABBC£ΩBHDB£¨º¥ABBC£Ω![]() BD2£¨Ω·∫œABBC£ΩAC2Õ∆≥ˆ
BD2£¨Ω·∫œABBC£ΩAC2Õ∆≥ˆ![]() BD2£ΩAC2£¨æð¥Àø…µ√¥∞∏£Æ
BD2£ΩAC2£¨æð¥Àø…µ√¥∞∏£Æ
Ω‚£∫£®1£©°þ°˜ABC «±»¿˝»˝Ω«–Œ£¨«“AB£Ω2°¢BC£Ω3£¨
¢Ÿµ±AB2£ΩBCAC ±£¨µ√£∫4£Ω3AC£¨Ω‚µ√£∫AC£Ω![]() £ª
£ª
¢⁄µ±BC2£ΩABAC ±£¨µ√£∫9£Ω2AC£¨Ω‚µ√£∫AC£Ω![]() £ª
£ª
¢€µ±AC2£ΩABBC ±£¨µ√£∫AC2£Ω6£¨Ω‚µ√£∫AC£Ω![]() £®∏∫÷µ…·»•£©£ª
£®∏∫÷µ…·»•£©£ª
À˘“‘µ±AC£Ω![]() ªÚ
ªÚ![]() ªÚ
ªÚ![]() ±£¨°˜ABC «±»¿˝»˝Ω«–Œ£ª
±£¨°˜ABC «±»¿˝»˝Ω«–Œ£ª
£®2£©¢Ÿ°þAD°ŒBC£¨
°ý°œACB£Ω°œCAD£¨
”÷°þ°œBAC£Ω°œADC£¨
°ý°˜ABC°◊°˜DCA£¨
¢⁄”…¢Ÿ÷™£¨°˜ABC°◊°˜DCA£¨
°ý![]() £¨º¥CA2£ΩBCAD£¨
£¨º¥CA2£ΩBCAD£¨
°þAD°ŒBC£¨
°ý°œADB£Ω°œCBD£¨
°þBD∆Ω∑÷°œABC£¨
°ý°œABD£Ω°œCBD£¨
°ý°œADB£Ω°œABD£¨
°ýAB£ΩAD£¨
°ýCA2£ΩBCAB£¨
°ý°˜ABC «±»¿˝»˝Ω«–Œ£ª
£®3£©»ÁÕº£¨π˝µ„A◊˜AH°ÕBD”⁄µ„H£¨

°þAB£ΩAD£¨
°ýBH£Ω![]() BD£¨
BD£¨
°þAD°ŒBC£¨°œADC£Ω90°„£¨
°ý°œBCD£Ω90°„£¨
°ý°œBHA£Ω°œBCD£Ω90°„£¨
”÷°þ°œABH£Ω°œDBC£¨
°ý°˜ABH°◊°˜DBC£¨
°ý![]() £¨º¥ABBC£ΩBHDB£¨
£¨º¥ABBC£ΩBHDB£¨
°ýABBC£Ω![]() BD2£¨
BD2£¨
”÷°þABBC£ΩAC2£¨
°ý![]() BD2£ΩAC2£¨
BD2£ΩAC2£¨
°ý![]() £Ω
£Ω![]() £Æ
£Æ

 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏