题目内容
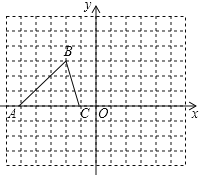
【题目】在一条公路上顺次有![]() 、
、![]() 、
、![]() 三地,甲、乙两车同时从
三地,甲、乙两车同时从![]() 地出发,分别匀速前往
地出发,分别匀速前往![]() 地、
地、![]() 地,甲车到达
地,甲车到达![]() 地停留一段时间后原速原路返回,乙车到达
地停留一段时间后原速原路返回,乙车到达![]() 地后立即原速原路返回,乙车比甲车早1小时返回到
地后立即原速原路返回,乙车比甲车早1小时返回到![]() 地,甲、乙两车各自行驶的路程
地,甲、乙两车各自行驶的路程![]() (千米)与时间
(千米)与时间![]() (小时)(从两车出发时开始计时)之间的函数图像如图所示.
(小时)(从两车出发时开始计时)之间的函数图像如图所示.
(1)甲车到达![]() 地停留的时间为 小时;
地停留的时间为 小时;
(2)求甲车返回![]() 地的图中
地的图中![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)直接写出两车在图中相遇时![]() 的值.
的值.
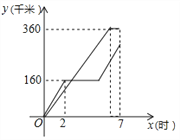
【答案】(1)3;(2)y=80x-240;(3)两车在途中相遇时x的值为![]() 或
或![]() .
.
【解析】试题分析:(1)根据甲的行进方式,观察图象,可知时间.(2)利用待定系数法求一次函数解析式.(3)分别求出甲乙速度,第一次第二次相遇分别计算.
试题解析:
(1)由图象知3小时.
(2)设y=kx+b,图象过(5,160),(7,320),
![]() ,解得
,解得![]() .
.
甲车返回A地图中y与x之间的关系是y=80x-240.
(3)由题意得,
甲车速是160![]() 千米/时.
千米/时.
乙车的车速是360![]() 千米/时.
千米/时.
第一次相遇时间是160![]() =
=![]() 小时.
小时.
第二次相遇时间是x,(360-60x)=160,(360-60x)=320-(80x-240),
解x=![]() ,x=10(舍去).
,x=10(舍去).
所以相遇时是![]() ,
, ![]() ,小时.
,小时.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
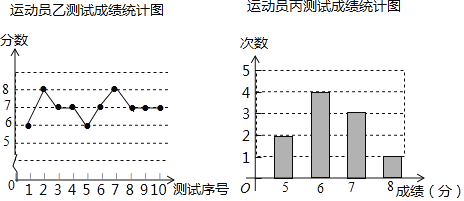
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么? (参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)