题目内容
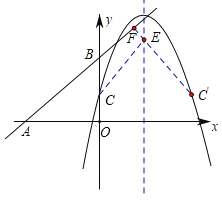
【题目】已知:如图,直线y=kx+b(k,b为常数)分别与x轴、y轴交于点A(﹣4,0),B(0,3),抛物线y=﹣x2+4x+1与y轴交于点C,点E在抛物线y=﹣x2+4x+1的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( )

A.2B.4C.2.5D.3
【答案】B
【解析】
设C点关于抛物线对称轴的对称点为C′,由对称的性质可得CE=C′E,则可知当F、E、C′三点一线且C′F与AB垂直时CE+EF最小,由C点坐标可确定出C′,F点的坐标,即可求得CE+EF的最小值.
解:如图,设C点关于抛物线对称轴的对称点为C′,由对称的性质可得CE=C′E,
∴CE+EF=C′E+EF,
∴当F、E、C′三点共线且C′F⊥AB时CE+EF最小,
∵直线y=kx+b(k,b为常数)分别与x轴、y轴交于点A(﹣4,0),B(0,3),
∴![]() ,
,
解得![]() ,
,
∴直线解析式为y=![]() x+3;
x+3;
∵抛物线y=﹣x2+4x+1与y轴交于点C,
∴C(0,1),
∴C′(4,1),
∴可设直线C′F的解析式为y=﹣![]() x+
x+![]() ,
,
由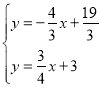 ,解得
,解得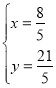 ,
,
∴F(![]() ,
,![]() ),
),
∴C′F= =4,
=4,
即CE+EF的最小值为4,
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目