Question

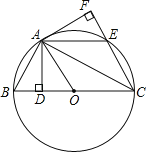
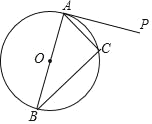
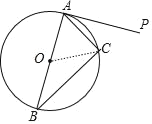
【题目】如图，△ABC为⊙O的内接三角形，其中AB为⊙O的直径，过点A作⊙O的切线PA．

（1）求证：∠PAC＝∠ABC；

（2）若∠PAC＝30°，AC＝3，求劣弧AC的长．

Answer 1

【答案】（1）详见解析；（2）π.

【解析】

(1)根据直径所对的圆周角是直角可得∠ACB＝90°，根据切线的性质可得∠BAP＝90°，由此即可求得答案；

(2)连接OC，证明△AOC是等边三角形，继而根据弧长公式进行求解即可.

(1)∵AB是直径，

∴∠ACB＝90°，

∵PA是⊙O切线，

∴OA⊥PA，

∴∠BAP＝90°，

∴∠PAC+∠BAC＝90°，∠BAC+∠B＝90°，

∴∠PAC＝∠B．

(2)连接OC，

∵∠PAC＝30°，

∴∠B＝∠PAC＝30°，

∴∠AOC＝2∠B＝60°，

∵OA＝OC，

∴△AOC是等边三角形，

∴OA＝AC＝3，

∴的长＝＝π.