Question

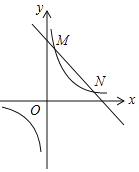
【题目】如图，一次函数y1＝kx+b（k，b为常数，k≠0）的图象与反比例函数y2＝（m为常数，m≠0）的图象相交于点M（1，4）和点N（4，n）．

（1）反比例函数与一次函数的解析式．

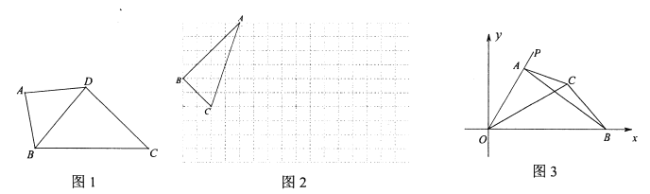
（2）函数y2＝的图象（x＞0）上有一个动点C，若先将直线MN平移使它过点C，再绕点C旋转得到直线PQ，PQ交x轴于点A，交y轴点B，若BC＝2CA，求OAOB的值．

Answer 1

【答案】（1）y＝，y＝﹣x+5；（2）OAOB的值为18或2．

【解析】

（1）将点M（1，4）代入y2＝（m为常数，m≠0）求反比例函数解析式，再求得N的坐标，将M与N两点坐标代入y1＝kx+b，即可求解；

（2）过C作CH⊥y轴于点H，分三种情况结合三角形相似可求得OA和OB的值，则可求得OAOB．

（1）将点M（1，4）代入y2＝（m为常数，m≠0），

∴m＝1×4＝4，

∴反比例函数的解析式为y＝，

将N（4，n）代入y＝，

∴n＝1，

∴N（4，1），

将M（1，4），N（4，1）代入y1＝kx+b，

得到，

∴，

∴一次函数的解析式为y＝﹣x+5；

（2）设点C（a，b），则ab＝4，过C点作CH⊥OA于点H．

①当点B在y轴的负半轴时，如图1，

∵BC＝2CA，

∴AB＝CA．

∵∠AOB＝∠AHC＝90°，∠OAB＝∠CAH，

∴△ACH∽△ABO．

∴OB＝CH＝b，OA＝AH＝a，

∴OAOB＝ab＝2．

②当点B在y轴的正半轴时，

如图2，当点A在x轴的正半轴时，

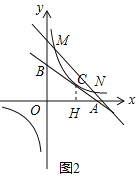
∵BC＝2CA，

∴

∵CH∥OB，

∴△ACH∽△ABO．

∴

∴OB＝3b，OA＝a

∴；

③当点A在x轴的负半轴时，BC＝2CA不可能．

综上所述，OAOB的值为18或2．