Question

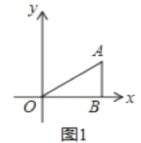
【题目】如图1,在平面直角坐标系中,点O为坐标原点,点A(3a,2a)在第一象限,过点A向x轴作垂线,垂足为点B,连接OA,S△AOB=12，点M从O出发，沿y轴的正半轴以每秒2个单位长度的速度运动，点N从点B出发以每秒3个单位长度的速度向x轴负方向运动，点M与点N同时出发，设点M的运动时间为t秒，连接AM，AN，MN.

(1)求a的值；

(2)当0<t<2时，

①请探究∠ANM，∠OMN，∠BAN之间的数量关系，并说明理由；

②试判断四边形AMON的面积是否变化?若不变化，请求出其值；若变化，请说明理由。

(3)当OM=ON时，请求出t的值。

Answer 1

【答案】（1）a=2；（2）①∠ANM=∠OMN+∠BAN，理由见解析. ②四边形AMON的面积不变，理由见解析. （3）t= 或6

【解析】

1）根据△AOB的面积列出方程即可解决问题；

（2）当0<t<2时①∠ANM=∠OMN+∠BAN．如图2中，过N点作NH∥AB，利用平行的性质证明即可．②根据S四边形AMON=S四边形ABOM-S△ABN，计算即可；

（3）由OM=ON，得到2t=63t或2t=3t6，求出答案.

(1)如图1中，

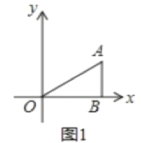
∵S△AOB=12,A(3a,2a)，

∴ ×3a×2a=12，

∴a =4，

又∵a>0，

∴a=2.

(2)当0<t<2时

①∠ANM=∠OMN+∠BAN，原因如下：

如图2中,过N点作NH∥AB，

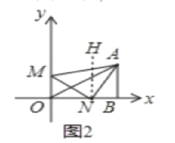
∵AB⊥X轴

∴AB∥OM

∴AB∥NH∥OM

∴∠OMN=∠MNH

∠BAN=∠ANH

∴∠ANM=∠MNH+∠ANH=∠OMN+∠BAN.

②S四边形AMON=12，理由如下：

∵a=2

∴A(6,4)

∴OB=6，AB=4，OM=2tBN=3t

ON=63t

∴S四边形AMON=S四边形ABOMS△ABN,= (AB+OM)×OB×BN×AB= (4+2t)×6×3t×4=12+6t6t=12，

∴四边形AMON的面积不变

(3)∵OM=ON

∴2t=63t或2t=3t6

∴t= 或6.